Quaternion Interpolation

[sybren]

Hello all,

Quaternion interpolation in Blender is an area that many people would like to see improved. This thread is meant to discuss low-level, behind-the-scenes improvements to Blender.

Recently there was a discussion on the topic per email between Brecht van Lommel (@brecht), Stefan Werner (@StefanW) and Mark Theriault from Tangent Animation, and me. I’ll try and summarize the discussion, so that it can be continued here with a wider audience.

I have marked certain phrases in bold. I’m not yelling or saying that these are more important than anything else. It’s just to aid scannability of the text.

The Problem

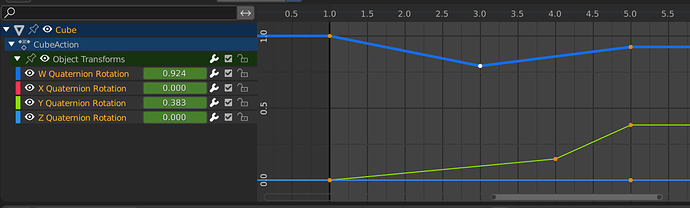
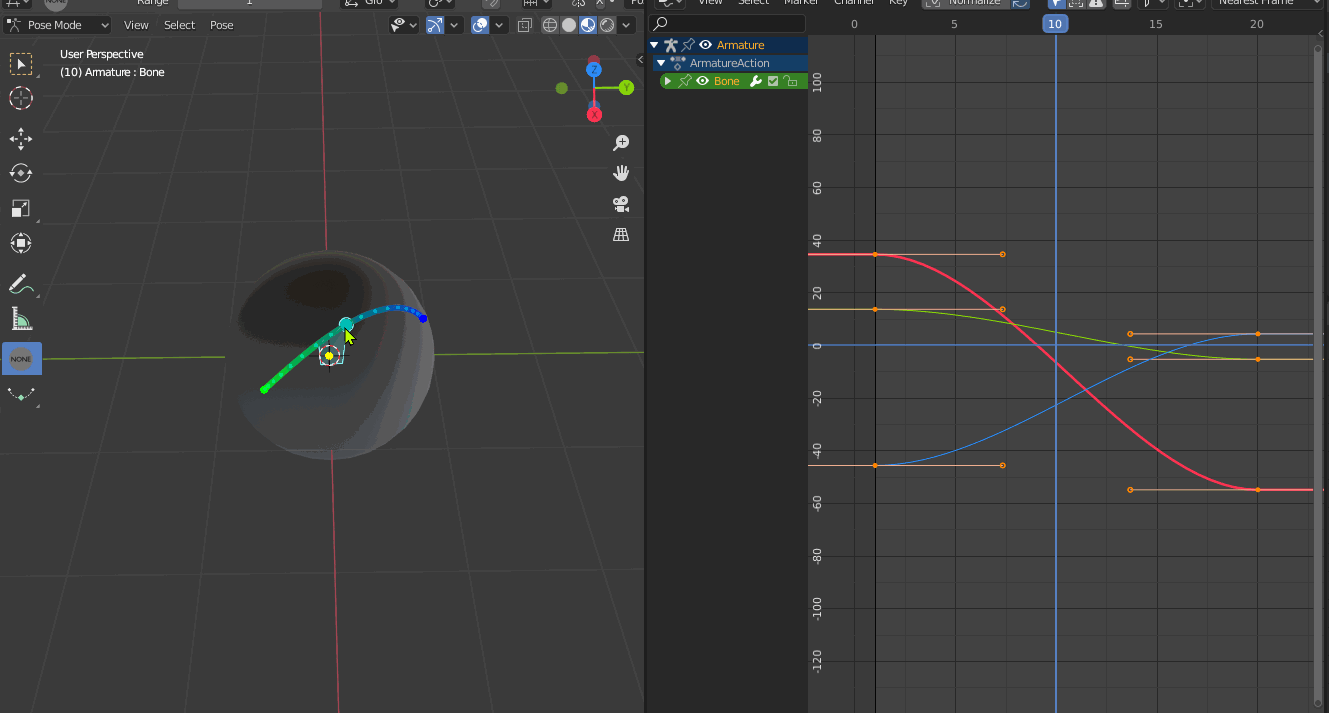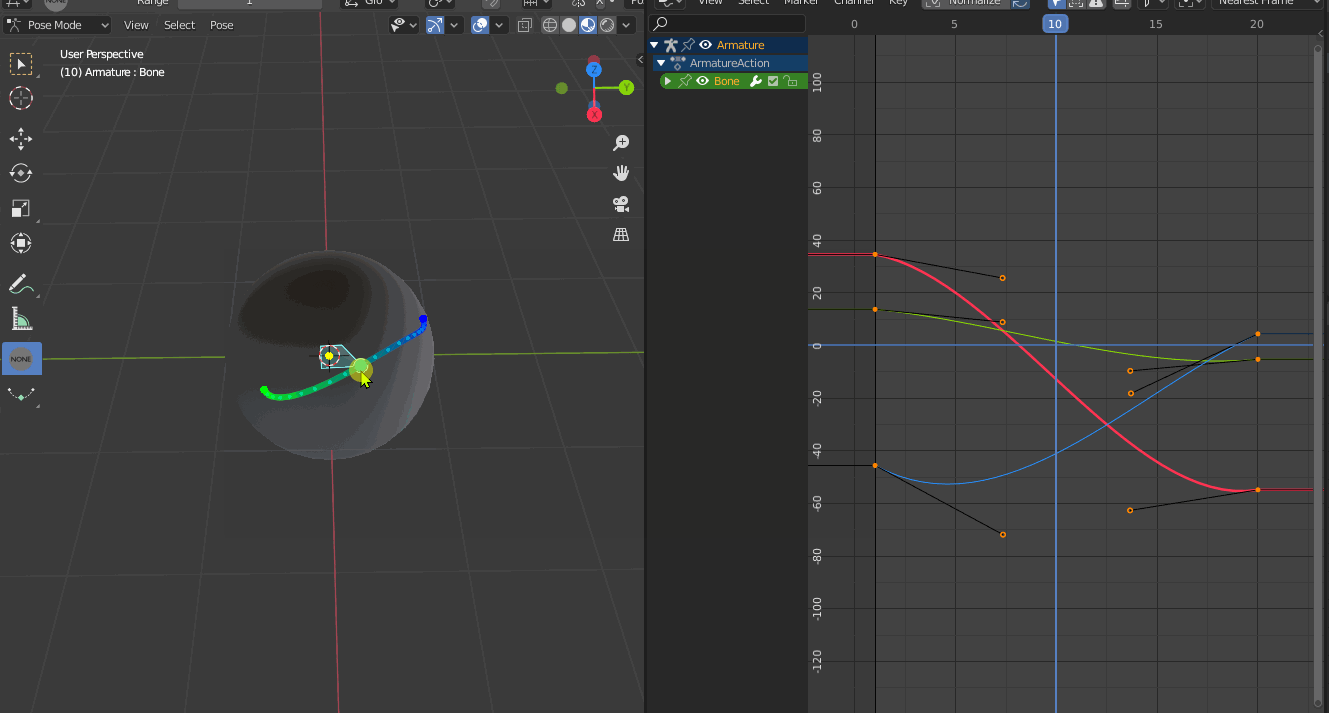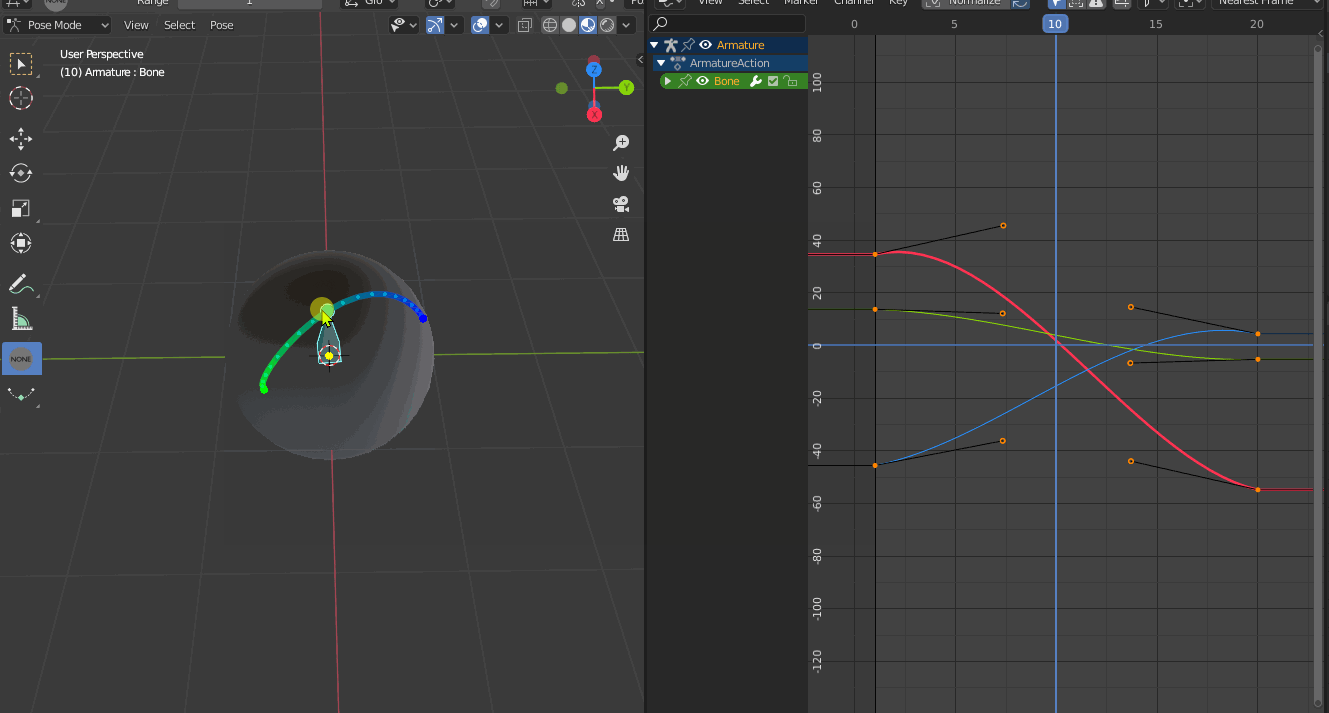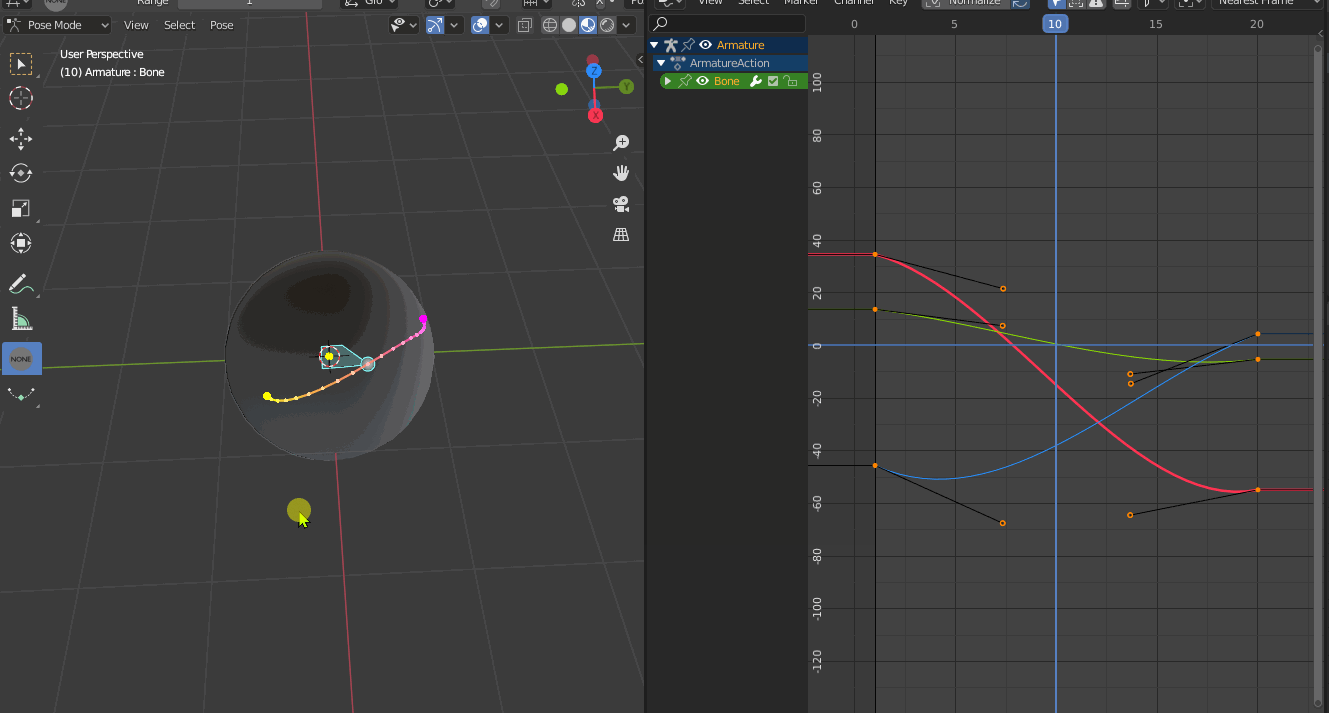
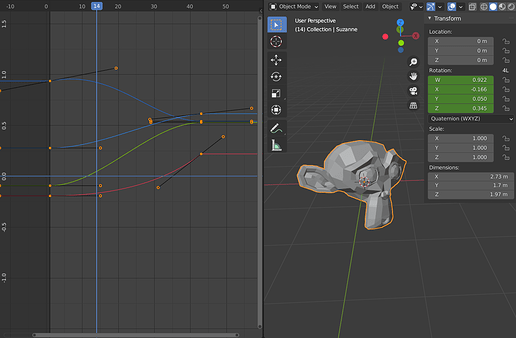
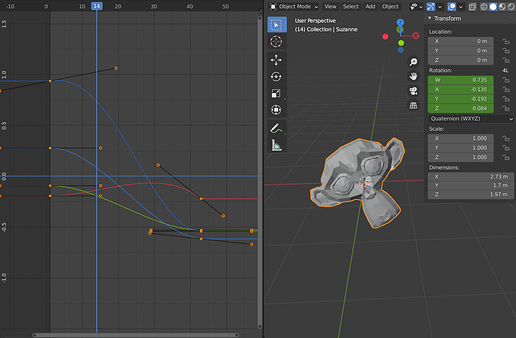
The problem is that Blender only performs component-wise interpolation (T45473), even when interpolating between quaternions. This causes interpolation artefacts. Even when you key every frame, interpolation is still necessary to properly render motion blur.

The underlying technical issue is that animation evaluation assumes that each FCurve can be interpolated individually.

The Solution

The solution is to make Blender use spherical interpolation for quaternions. This category can be split up into linear A-to-B interpolation (SLERP) and quadratic A-via-B-to-C interpolation (SQUAD).

Previous Attempt

There is an old patch (D1929, 2016) that adds SLERP/SQUAD as new rotation modes (so you have the choices Quaternion, Quaternion SLERP, and Quaternion SQUAD). However, Josua Leung points out that the patch

• only works for FCurves in the current Action of a datablock, and not for any NLA strips that could provide other animation or modify the existing animation,
• doesn’t take FCurve Modifiers into account,
• only works for bones,
• has problems with drivers,
• doesn’t allow animators control over the speed at which rotations are approached, and
• it is unknown how it works with action constraints, motion paths, or manual tweaks to the curves.

I think these are all valid concerns for any solution.

Brecht’s suggestion

In our email discussion, @brecht writes (emphasis mine):

What needs to be done is refactoring the code to remove the assumption that you can simply call evaluate_fcurve(fcurve, time) and get a float value for an individual curve.

The simplest solution would be to find the other f-curve for the quaternion in fcurve_eval_keyframes, and then use them for SLERP. You could quickly hack this in by just following the next/prev pointers in the f-curve, the quaternion components should be consecutive in the list in practically all cases (but I’m not entirely sure that’s something that is guaranteed, it could be enforced if so).

Of course that means performance will not be ideal, the same curves will be evaluated 4x. The most performance-critical case is animation playback where we evaluate all f-curves in a single function, so avoiding it there should not be hard with some refactoring. For other random tools and Python API access, performance may either not be critical, or there could be a local cache (passed to evaluate_fcurve as an argument) knowing that quaternion components are likely to be evaluated consecutively.

and after I voiced concern about drawing the curves in the Graph Editor:

There is a code path that uses the bezier curves directly, and one that calls evaluate_fcurve for every time step, which is slower but needed for modifiers. The quaternion case could be made to use the slower call. The proper abstraction here would be to have a version of evaluate_fcurve that can evaluate multiple samples in a time range with whatever optimizations are possible depending on the type of f-curve.

Concerns about Invalid Quaternions

@StefanW voiced his concerns over the fact that having control over the FCurves for individual quaternion components can produce mathematically invalid quaternions. I had the same concerns: it is even possible to have different interpolation options (constant, linear, bouncy etc.) for each component. Although this is true, there is also a strong desire from animators to keep per-component control, at least until there is something that works better. For now we’ll just have to normalise the quaternions before interpolation.

Steps forward

I think that Brecht’s suggestion is a good one to try and implement first.

• Existing animation should not be broken. This means that animators must have a choice over Blender’s current behaviour vs. spherical interpolation, for example via an FCurve setting. This setting could be synced between the four FCurves of a single quaternion.
• fcurve_eval_keyframes is altered to do SLERP. Open for discussion is how to handle the case when not all w/x/y/z channels are keyed simultaneously.
• Force Actions to have their FCurves sorted, at least such that curves on the same RNA path are consecutive and ordered by array index.
• Improve animation evaluation to only SLERP once per quaternion, and not once per FCurve.

[GuiltyGhost]

@sybren

fcurve_eval_keyframes is altered to do SLERP. Open for discussion is how to handle the case when not all w/x/y/z channels are keyed simultaneously .

A potential solution might be to temporarily insert a keyframe on the channel that lacks the keyframe. The inserted keyframe should preserve the curve’s shape (https://developer.blender.org/D3172). Then you can slerp as normal as if all keys existed. That solution would work for normal FCurves. Though I don’t have much Quaternion math experience so I’m not 100% sure if the solution extends to Quaternions.

Edit: This case may also be unlikely too. If anyone can explain a realistic use case for having missing keyframes, I’d like to know. Until then, I think it would be fine to handle this case by falling back to the current interpolation method.

[Cessen]

@sybren

@StefanW voiced his concerns over the fact that having control over the FCurves for individual quaternion components can produce mathematically invalid quaternions .

From a purely math perspective, I believe this concern is unfounded. My guess (?) is that this is coming from the perspective that Blender ought to directly use the fcurve values when computing quaternion rotations. But I see no reason that ought to be the case.

Blender currently normalizes (and I believe always has normalized?) quaternion values before applying them as rotations, which ensures mathematical validity.

I think that’s actually a really nice way to approach things. Instead of working in a fragile 4d space where only a narrow 3d manifold (the surface of the unit hypersphere) is valid, it allows us to work in a forgiving 4d space where all points are treated as valid by projecting them onto valid points. It’s a really simple and IMO elegant solution to working with quaternion rotations, and it provides a level of flexibility to users that no other approach I’m aware of does.

Having said that, I definitely agree that this approach also has drawbacks. I would really like to see other approaches for handling quaternion rotations added to Blender. But I want to warn against seeing the current approach as somehow mathematically invalid or incorrect, because 1. that’s simply not the case and 2. thinking that way may actually push us away from other valid and worthwhile solutions.

So I would really like to encourage everyone to discuss the properties and benefits/drawbacks of various approaches, without writing them off as intrinsically incorrect (unless, of course, they actually are).

[Cessen]

To follow my own advice, the main drawbacks I’m aware of the current approach having are:

1. It isn’t generally capable of rotating at a constant velocity like e.g. slerp. For key frames <= ~90 degrees apart, the velocity variance is generally minor enough to not matter. But for larger rotations it can definitely become an issue.

2. Treating the four components as completely unrelated data prevents us from doing nice things like ensuring that at least at key frames the quaternions are properly normalized, which would make them much nicer to work with (even if we still interpolated per-component).

3. Even if we treat the four components as related, if we still treat them as separate curves then we can’t do nice things like ensuring that interpolation always takes the shortest path, which is a nicer behavior for animators to work with.

Issues #2 and #3 aren’t intrinsic to a per-component interpolation approach, but they are intrinsic to exposing the curves to be independently manipulated by the user. Issue #1 is the only issue I’m aware of that is actually intrinsic to the interpolation approach itself.

The main benefits of the current approach (that I’m aware of) are:

1. Performance. Simple per-component interpolation is faster than slerp/squad/etc. I don’t think this is actually a major concern, but for heavier scenes it might make a difference. Not sure.

2. It’s the only practical way (that I’m aware of) to expose the individual quaternion components to the user for arbitrary manipulation without breaking the math. For animation this may become obsolete as better approaches are added, but for rigging I think erring on the side of allowing low-level access like this whenever possible is a good thing.

3. It makes it really straightforward to apply the same tools to quaternions as other animation curves (e.g. working with tangent handles, applying fcurve modifiers, etc.). Other approaches will hopefully also allow for this, but naively adding slerp and squad won’t.

Of these, I think #2 is the most important benefit. I think #3 is also important in the short-to-mid-term, but I’m excited about finding alternate ways to work with rotations (and perhaps transforms generally) that would make #3 more-or-less obsolete.

[sybren]

@Cessen

From a purely math perspective, I believe this concern is unfounded. My guess (?) is that this is coming from the perspective that Blender ought to directly use the fcurve values when computing quaternion rotations. But I see no reason that ought to be the case.

I think it’s just the difference of views between @StefanW’s “can produce invalid quaternions”, which is true, and your “there are ways around this”, which is also true.

@GuiltyGhost

A potential solution might be to temporarily insert a keyframe on the channel that lacks the keyframe. The inserted keyframe should preserve the curve’s shape. Then you can slerp as normal as if all keys existed.

This would be the same as simply evaluating the curve at that point. I don’t think this’ll be mathematically sound, though. Let me illustrate.

Take this example, in which I rotate the default cube from its zero orientation (frame 1) to 45° along the Y-axis (frame 5). I then went in and tweaked the W component (frame 3) and Y component (frame 4). I have set all interpolation to linear so that we don’t have to bother with handles.

Now, to compute the orientation at frame 4, we need a value for the W-component. We could indeed just evaluate its curve, get the W-component (and the other unkeyed values), and normalise to get the quaternion. But that would LERP at that point. SLERPing between frames 3 and 5 would produce a different W-value (i.e. the value we actually want to have).

You could attempt to solve this by actually doing a SLERP between frames 3 and 5. However, that then produces the same issue, that the non-W components aren’t well-defined on frame 3. Of course, you can do a SLERP between frames 1 and 5 for the X and Z components, but you’d have to do a SLERP between frames 1 and 4 to get the Y-component, and that’s where we’re back at needing the values for frame 4.

I think the “easiest” solution would be to actually require all components of a quaternion to be keyed simultaneously when SLERP is enabled. Blender could help animators by either automating & enforcing this, or by highlighting areas of the graph editor where this is not the case.

Blender can fall back to LERP where SLERP is not possible, but I feel that this should be accompanied by an indication that some fallback behaviour has been activated. If the animator asks for SLERP, Blender should SLERP or be explicit in that it can’t (and why, and how to solve).

PS: for the implementation of SLERP we may decide to not implement it as traditional SLERP, but more like described by Jonathan Blow, Hacking Quaternions, 2002 (also see Jonathan Blow, Undertanding Slerp and then not using it, 2004; thanks @Cessen for sharing both).

[Cessen]

@sybren

I think it’s just the difference of views between @StefanW’s “ can produce invalid quaternions”, which is true, and your “there are ways around this”, which is also true.

I agree that it comes down to a difference in perspective, but I think the difference is an important one. For example, even here you (edit: I think unintentionally) reinforce the “it’s invalid” perspective by reframing my argument as “there are ways around this”, giving an impression that the current solution is a work-around or hack, which is simply not the case.

I won’t belabor the point any further, though, as I’ve already made my case. But I want to re-emphasize my conclusion so that it cannot be mistaken: Blender’s current approach is perfectly valid, mathematically sound, and is not just a work-around or hack. It is an elegant solution to interpolating and working with quaternion rotations.

[Cessen]

@sybren

I think the “easiest” solution would be to actually require all components of a quaternion to be keyed simultaneously when SLERP is enabled. Blender could help animators by either automating & enforcing this, or by highlighting areas of the graph editor where this is not the case.

Backwards compatibility aside, I think this would be a good thing even with the current interpolation approach. In particular it would allow (at least by default) enforcement of the keyframes themselves being normalized, which generally makes quaternion rotations easier to work with.

Back when working on Big Buck Bunny, Blender actually auto-normalized quaternions when inserting keys, which made it feasible to essentially “sculpt” the rotation paths and ease-in-ease-out by just inserting more keys and moving them around in the dopesheet. That workflow, while not impossible now, certainly isn’t nearly as effective as it used to be in 2.49 and earlier.

[JackCai]

Instead of overriding existing quaternion, can we added a new field, maybe something like “unit quaternion” in addition to Euler and existing quaternion and design UI specific for it?

Some wild ideas like this as a read/view-only widget in the editor. We don’t need to do path editing like in this gif, just showing the path on the unit sphere is great. Just visual assistance. This sphere will always move with the object such that it is not really the motion path. This unit sphere can be scaled as well to see more subtle rotations.

In the graph editor, we could have the Both the X and Y value of each key to be the frame number, and the actual quaternion value is shown as some kind of annotation around the key icon or in the side panels or just shown in the viewport like above, and then in between keyframes just show how fast 1 key transition to the other.

Given this, say if there are unit quaternion keys on the 0th frame and the 5th frame.
In the graph editor:

1. SLERP between these two keys will just show a 45-degree straight line connecting (0,0) and (5,5).
2. Traditional linear interpolation will just be an “S” shaped curve connecting (0,0) and (5,5)

These are probably the wildest ideas, hope more people join in on the conversation drag me back down to a more feasible and realistic solution to this problem.

[StefanW]

@Cessen

Blender’s current approach is perfectly valid, mathematically sound , and is not just a work-around or hack. It is an elegant solution to interpolating and working with quaternion rotations.

There are two problems that I see with lerping quaternions:

1. You can get interpolated values of (0, 0, 0, 0), that is, entirely invalid values that can not be salvaged by normalizing. Since quaternions allow two different representations of the same orientation, you can have a seemingly static object do a sudden jump at just a single frame. Example: Suzanne in an otherwise empty scene. Set a w=1, xyz=0 key at frame 1, a w=-1, xyz=0 key frame at frame 13. Now play back the animation - Suzanne will be static except for a sudden flip at frame 7. You could try and hide this manually by inserting extra key frames, but this will only work if you’re not using motion blur, where sub-frames are evaluated too.

2. It is not using the shortest path on a sphere. While this is a desirable property for Euler angles and allows one to do rotations of more than 360 degrees between keyframes, the restriction of no more than two turns makes it less useful for quaternions. Again, this is something that can hide in subframes - we’ve had, in production, animation that looked perfect in an OpenGL playblast, but when rendered with motion blur showed erratic steaks at seemingly random frames that turned out to be rotations interpolated “the long path” between two key frames.

This is why I think the current interpolation is something that works most of the time for most people, but has corner cases in which it fails very visibly. The only workaround I could come up with would be to forcibly break the interpolation by inserting constant key frames, but that requires tracking down every single instance where those unwanted interpolations happen. I don’t think that this is a practical solution. Neither for they hobbyist who may not have the necessary mathematical understanding of quaternions, nor to the big studio that would have to find needles in a haystack when it comes to complex rigs with hundreds of key frames.

I’m not denying that lerp and direct access is useful to you - I’m all for allowing technical users to go wild - but at the moment I think quaternions are not predictable or fail safe enough to be useful to everyone.

[Cessen]

I 100% agree with you about the problems you’ve described with Blender’s quaternion rotation implementation. But I believe their source is different than what you’re ascribing them to. More below.

@StefanW

You can get interpolated values of (0, 0, 0, 0), that is, entirely invalid values that can not be salvaged by normalizing.

While that’s true, the situation where that comes up is also a failure case for slerping. Specifically: interpolating between opposite quaternions. And the fix is the same for both slerp and lerp: checking the dot product of the two quaternions, and flipping one of them before interpolating if they’re on opposite sides of the hypersphere.

@StefanW

It is not using the shortest path on a sphere.

Again, in the general case this is not true of slerp either. Slerp is usually implemented with the above-described dot-product check, but that’s not actually part of the slerp interpolation math. And that same check can be applied to per-component interpolation as well.

Part of what I’m trying to do in this thread is make a distinction between the interpolation math used (e.g. slerp vs per-component) and how the data is wrangled and presented to the user (e.g. exposing individual curves, letting the wxyz components be keyed on different frames, etc.). The latter is actually the core source of the problems, because it prevents doing things like that dot-product-check-and-flip: you can’t do that if the wxyz components can be keyed on different frames, for example.

I have a proposal that I’m (slowly) writing up that I believe addresses these (and other) issues in a nice way. I’ll try to post it soon.

[StefanW]

@Cessen

While that’s true, the situation where that comes up is also a failure case for slerping. Specifically: interpolating between opposite quaternions. And the fix is the same for both slerp and lerp: checking the dot product of the two quaternions, and flipping one of them before interpolating if they’re on opposite sides of the hypersphere.

The problem with the current implementation in Blender is (and you’re probably aware of this, just explaining it once more for everyone reading along) that at the time of interpolation, it is not aware of quaternions. It is interpolating four completely independent float fCurves. Only once those fCurves are evaluated, the four resulting float values are interpreted as a quaternion. The original data from which it was interpolated is not available at that point - it can’t check dot products.

Once we have that changed, and Blender is at the time of interpolation aware that it’s dealing with a quaternion and not four independent floats, then we can throw in a simple dropdown menu to pick between lerp, slerp or any other method.

[Cessen]

100% in agreement there. And that’s a part of my upcoming proposal.

[StefanW]

I’m looking foward to it. My main complaint is/was not lerp vs slerp (I’ll let the animators decide which one they prefer) but that the per-component interpolation is oblivious to the fact that a quaternion is not four independent floats.

[Cessen]

Here is my proposal for how quaternions in Blender could work moving forward.

Core proposal

The core of the proposal is to add a single new quaternion rotation mode, like so:

…with the following properties:

1. Blender internally recognizes the WXYZ channels as being associated.
2. Key frames are always on WXYZ together. In other words, having different channels keyed on different frames isn’t possible.
3. Key frames are enforced to be normalized. (But segments between key frames are not).

I think these three properties together allow some really nice things, and provide a lot of flexibility for designing how things work.

The remainder of this proposal is one way things could work within that core, and I think helps illustrate the advantages that fall out of it. But I hope this can be a jumping off point for further discussion and refinement. (Having said that, the following isn’t a throw-away proposal by any means.)

Per-segment interpolation modes

Standard fcurves allow users to interpolate different parts of the curve differently. For example, one segment can be linear, another constant, and another spline. It all works together nicely because all keys are valid for any interpolation approach.

By enforcing that all quaternion channels are keyed together and are normalized at those keys, we get the same benefit with quaternions. One segment can be constant, another slerp, and another per-component spline, and it all works together.

I think this is a more practical and useful solution than having completely different quaternion modes for each type of interpolation, and it also keeps quaternions working more like other curves, making things less jarring for users.

Quaternions as quaternions

I propose that we still display quaternions as WXYZ in the fcurves editor, n-panel, etc. Blender would enforce normalization when tweaking those values by hand.

The main concern with exposing quaternions as quaternions like this is that it potentially gets in the way of shortest-path interpolation. But I believe there’s a reasonable solution to that (see the section below).

Additionally, visualizing things as the actual WXYZ values makes it easy for users to tweak the tangents of spline segments, and it potentially even enables the use fcurve modifiers (sometimes useful for e.g. adding jitter/wobble).

Shortest-path interpolation

Always taking the shortest rotation path when interpolating is desirable, as it avoids a host of issues including (as outlined clearly by @StefanW):

1. Preventing ill-formed interpolation situations (specifically, interpolating between opposite quaternions).
2. Preventing accidental sub-frame long-way-around interpolations.

It also generally provides a more intuitive way for animators to work, who ideally shouldn’t need specific education about double-cover and its properties.

However, exposing the WXYZ values seems to preclude shortest-path interpolation. For example, consider the following animation curves:

This is a (per-component) spline interpolation between two quaternion keys, and already takes the shortest path. If we flip one of the quaternions, however, we get this:

This is now interpolating the long way around. At first glance, it seems impossible to take the shortest-path interpolation here while still displaying the quaternion values as they actually are. However, there is a solution: allow discontinuities in the curves:

(Actual visualization of the discontinuity very open to improvement.)

This might seem ugly, and… it is. But there actually is a discontinuity in quaternion space is these cases, so it’s representing things accurately. Moreover, discontinuities are already a part of fcurves in the form of constant interpolation, so it isn’t introducing anything new in that sense.

I personally prefer this from a visualization standpoint, as it provides an opportunity for users to understand what’s happening with the real data if they want to. But more important than the visualization is what it enables practically:

• We can still work with quaternions as quaternions.
• We can include all interpolation approaches (constant, lerp, etc.) within the same animation curve.
• Animators can still adjust tangent curves and other data where relevant.
• Fcurve modifiers can still be used.
• Possibly other things as well…?

Finally, it’s completely mechanical and lossless to fix these discontinuities by iteratively flipping quaternion keys (and their tangents) wherever discontinuities are encountered. We could even introduce an operator that does this automatically, similar in spirit to the Euler discontinuity filter.

What to do about squad?

(Edit: upon further poking around, it seems that what I’ve described below isn’t squad. I’ve always assumed it was, since it’s what’s described in the widely referenced Shoemake paper. With that in mind… I don’t think squad itself is actually useful, and what I’ve actually been referring to as squad is what I’ve described below. I’ll leave the below unedited.)

My initial thought when drawing up this proposal was that, at least for a first implementation, we would leave out squad, and just provide the following interpolation approaches:

• Constant
• Slerp (linear)
• Per-component spline.

I do think these three cover the practical animation use-cases. And you may notice as well that I’ve dropped lerp, since slerp covers its use-case strictly better.

But on further thought, I think some discussion about squad is needed before settling on any proposal (whether this one or another).

As a quick primer for anyone unfamiliar: squad is directly analogous to standard cubic bezier curve interpolation, but in spherical space. Given four unit quaternions start, handle_1, handle_2, and end, as well as an interpolation scalar t in [0, 1], you do the following:

a = slerp(start, handle_1, t)
b = slerp(handle_1, handle_2, t)
c = slerp(handle_2, end, t)
final = slerp(slerp(a, b, t), slerp(b, c, t), t)

(To further emphasize how analogous this is: if you replaced all the slerps above with lerps, you would have standard cubic bezier interpolation.)

The essential similarity of this to Blender’s standard fcurve splines makes it really tempting to just use this instead of per-component splines. And I think that’s a perfectly fine thing to propose–I’m halfway there myself. But there are some issues:

1. How can users work with the tangent handles? In particular, they have to be unit quaternions.
2. Are there meaningful performance implications here? Slerp is a bit computationally spendy, and here we’re doing six of them.
3. How do we calculate the tangent handles automatically? This is covered in the original paper “Animating Rotation with Quaternion Curves” by Ken Shoemake, but it doesn’t address things like “clamped auto” which are useful in practice for animators, but not (to me) obvious how to formulate in spherical space.

One possibility for issue 1 above is to just let the user manipulate the handles un-normalized, and normalize them before plugging them into the squad evaluation. Automatic handles would still produce normalized handles. I think this could work nicely.

For issue 2, there may be alternative formulations of squad that use fewer slerps (I’m not sure). And we could use a fast approximate slerp in the spirit of Hacking Quaternions or Approximating slerp. And knowing that all channels are keyed together, SIMD could potentially be employed as long as we avoid branching in our slerp approximation.

For issue 3, I don’t really have any specific thoughts yet.

Ultimately, I think this all comes down to the following question: does squad, in practice, have any properties that we care about over per-component splines? I think for the large majority of use-cases, the answer is no, as evidenced by animators getting along just fine without it up to this point. But there may be important niches, and maybe there are secondary things it would enable that are valuable.

Maybe it’s okay to punt on it for now, and just implement constant, slerp, and per-component spline first. And then if concrete use-cases show up for squad down the line, we can sort this out and implement it then. But it would be kind of unfortunate to ultimately end up with two confusingly similar interpolation approaches that users have to choose between.

Visualizations and tooling

Conspicuously absent from this proposal is anything about more sophisticated visualizations or tooling, such as viewport-based manipulation. This is on purpose. Not because I don’t think that would be useful (on the contrary). But rather because I think that can and should be layered on top of a more technical foundation like this that addresses the core technical issues.

Partly that’s simply because it seems feasible to do so, and addressing problems one-at-a-time is easier. But more importantly, it’s because those kinds of advanced visualizations and tooling apply to more than just quaternions or even rotations, and I think it would be better to address that in a holistic way that looks more broadly at how we want to enable people to work with animation.

[Cessen]

In my proposal above, I discussed what I thought was squad, but actually turned out to be a different interpolation approach. I also said in my edit that “I don’t think squad itself is actually useful”, which was overly curt and didn’t qualify what I really meant well enough.

Since then, I’ve done a further dive into quaternion rotation interpolation techniques. I certainly don’t fully understand everything I’ve encountered (in some cases the math is currently a bit beyond me), but I nevertheless want to share what I’ve found so far.

First off, although this is probably obvious, slerp is pretty much the “right” way to do linear interpolation for quaternion rotations, in the sense that it’s the only approach–by definition–that gives constant-speed rotation around a single axis. So that’s easy enough.

When you get into smooth interpolation, however, things get a lot more complex, and to some extent subjective. This shouldn’t be too surprising, since that’s the case in euclidean space as well: straight lines are obvious, but smooth interpolation has all kinds of approaches.

Squad

Squad, despite its name, is actually a cubic interpolation technique. The “quad” stands for “quadrangle”, not “quadratic”. It was introduced by Ken Shoemake in a 1987 paper entitled “Quaternion calculus and fast animation” that apparently is no longer available anywhere.

It takes an approach introduced by Wolfgang Boehm in “On cubics: A survey” for constructing cubic curves with only 3 lerps, and extends it straightforwardly to spherical space with slerps:

slerp(slerp(start, end, t), slerp(handle_1, handle_2, t), 2t(1 - t))

Although the Shoemake squad paper is no longer available, given its title I suspect the main motivation for proposing squad over other approaches was performance. It takes only 3 slerps compared to e.g. the 6 slerps of spherical bezier.

However, it doesn’t produce the same curve as a spherical cubic bezier curve. As far as I was able to determine from the papers I read (but take this with a grain a salt), the full cubic bezier produces visually smoother, more pleasing curves than squad. So it may be the case that squad is sort of the “poor man’s” spherical bezier, and its only benefit is execution speed.

Shoemake’s original spline construction equations (i.e. “auto” curves in Blender) for squad apparently have continuity issues: although the curve segments themselves are c2 (in fact, c-infinity), the composite splines are only c1. c2 is certainly not critical for auto-curves, but it is a nice-to-have and can be visually noticeable.

Spherical Cubic Bezier

This is the approach I mistakenly called squad, and is what Shoemake outlined in his earlier 1985 paper “Animating Rotation with Quaternion Curves”.

As mentioned above, it may produce nicer curves than squad, but it’s roughly twice as expensive to evaluate.

Just like squad, Shoemake’s spline equations for spherical cubic bezier are only c1-continuous.

RQBez

This is the approach that Blender currently uses. You do the interpolation with standard euclidean bezier curves, and re-normalize the resulting quaternions afterwards.

The paper “Survey of Higher Order Rigid Body Motion Interpolation Methods for Keyframe Animation and Continuous-Time Trajectory Estimation” by Haarbach et al. call this approach “Renormalized quaternion Bezier curve”, or “RQBez”.

Looking at the examples in that paper, IMO this approach actually produces nicer results than squad. In particular, the velocity acceleration/deceleration seems to be more uniformly smooth, whereas squad is kind of bouncy with sharp transitions at the keys.

Another potential benefit of RQBez is c2 continuity. The equations for c2 bezier splines in euclidean space are well known (and already implemented in Blender), and I think it’s the case that they remain c2 after normalization.

(My intuition behind that is it seems like projecting a c2 curve onto a c-infinity manifold like the hypersphere ought to preserve that continuity. But I’m not totally sure–someone please feel free to double-check. In any case, if that’s true, then we get c2 continuity without having to do anything special.)

This approach is also very performant, and it’s obvious how to implement “auto clamped”, etc.

Other Approaches

There are a whole bunch of other approaches for interpolating quaternions smoothly. A quick run-down of some papers that propose other methods:

• "A General Construction Scheme for Unit Quaternion Curves with Simple High Order Derivatives" by Kim et al. The method proposed here is a spline that is cubic, has c2 continuity, and doesn’t appear to be too much slower than squad. However, it doesn’t pass through its control points, which makes it unusable for animation interpolation.
• "Quaternion Cubic Spline" by McEnnan. This paper is beyond me (at least without spending a lot more time with it), but it does appear to propose a spherical spline that is c2 and passes through all points. I have no idea how tweakable it is by animators, however.
• "C2 spherical Bezier splines" by Popiel et al. I haven’t found a copy that’s not behind a paywall, but the abstract as well as the way it’s referenced in another paper suggests that it contains an approach for constructing c2-continuous splines from both squad and spherical cubic bezier curves. If someone wants to track this down, that would be awesome.
• "Quaternions, Interpolation and Animation" by Dam et al. This paper proposes an optimization-based approach to interpolating quaternions. It’s interesting, but I suspect we probably don’t want to use an interative optimization approach for animation interpolation.
• "Survey of Higher Order Rigid Body Motion Interpolation Methods for Keyframe Animation and Continuous-Time Trajectory Estimation" by Haarbach et al. They don’t propose any new methods in this paper, but as the name of the paper suggests they do provide a survey of rigid body interpolation approaches, the rotation component of which is all quaternion-based approaches.

Wrapping up

All-in-all, my impressions at this point are as follows:

• The solution-space for smooth quaternion rotation interpolation is complex, and there are a lot of competing approaches. They all seem to have pros and cons, and there isn’t a clear universal “winner”.
• Squad’s main selling point seems to be speed rather than quality. Importantly, it isn’t special compared to other approaches, and isn’t any kind of “natural” extension of slerp, despite the impression its name gives. If anything, the spherical cubic bezier approach is a more natural extension.
• The seemingly brain-dead RQBez approach actually appears to have some advantages, including speed, probably (?) c2 continuous splines, a straightforward f-curves workflow, and an obvious way to implement “auto clamped”.

Having said that, this was certainly not a thorough deep-dive into the subject matter, and I easily could have misunderstood some of the papers. As I said at that start of this post, the math involved in some of these papers is a bit beyond me at the moment.

[sybren]

It would be interesting to include the exponential map representation as well. That represents a rotation in R³, and all vectors are valid rotations. Basically it multiplies the rotation axis unit vector with the rotation angle. This representation makes it rather trivial to do weighted interpolations of multiple rotations. I’ve used this in my MSc graduation project Stride Space for exactly this purpose.