Why are curve normals called so when they should be called curve tangents?

Archive User Feedback
1

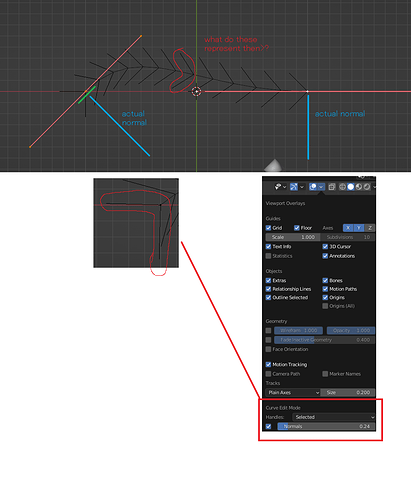
image
image968×1176 126 KB

We had a discussion on the blender discord and there was no answer that could be generated as well as a lot of confusion as to the naming convention. The arrowheads available with the viewport overlay don’t actually seem to represent the normals of the curve.

For instance, in the above imagine the position of normal vector for control point one is (0.707, -0.707, 0) and for the second control point it is (0,-1,0). These values have nothing to do with the arrowheads.

Reading the manual on ‘Curve display’
https://docs.blender.org/manual/en/latest/modeling/curves/curve_display.html

Normals
Toggles the display of the curve normals.

Once again, this term is confusing. If it is not representing visually, or displaying the curve normals in actuality, why is this naming convention used? For convenience? IT has been very confusing while using this in combination with geonodes. The representation is not accurate, and it might be worth changing the name to better reflect what it actual does represent (the tangent?)

2 Likes
2

I agree the naming is confusing. They are not tangents either though. More something like ‘direction arrows’ .

3

I think the devs just used the term “normals” here because the kind of stick out of the curve like normals would do (although of course unlike actual normals they aren’t actually normal to the curve).

However calling them curve tangents is also incorrect, in fact the red handle is the curve tangent by definition.

As to what the black lines called “normal” by Blender mean they have three meanings:

  1. The direction of the lines shows the direction of the curve, that is if you image the pair of lines as an arrow then they point form the beginning to the end of the curve.

  2. The length of the lines shows the radius of the curve. This is akin to the scale of objects.

  3. The rotation of the lines relative to the curve show the curve tilt. This is a little harder to explain. The problem is the following:
    As a 1D object a curve actually has infinitely many normals in 3D. But if we were to lets say use a curve modifier on a mesh to bring it onto the curve. The Deform Global Axis is provided by the user, Blender then has to decide for exactly one of the infinite possible normals to be one of the other Global Axis, let’s call it “reference normal”, the other is then calculated through the cross product of both.
    The user has the option to control the “reference normal” through the Tilt value (Ctrl T). The curve tangent, “reference normal”, and black line called “normal” are always coplanar (in the same plane) and the user can use the black line called “normal” to judge the “reference normal”.

As to what they are mathematically, you would have to look into the source code, but by the looks of it. it seems to be the angle bisector of the curve tangent and the curve normal.

1 Like