Once you add in proper black body radiators etc., the differences should become larger I think, though probably still very subtle
Yes, once we start making better use of spectra then we will see some larger differences, and hopefully more intuitive material creation.
Can this be done for any coordinate within the spectral locus? I’m trying to think what constraints would need to exist for a general purpose (any real colour) solution. If we can figure that out and run it for a whole bunch of colours, we could achieve the end goal of ‘good’ reflectance curves for any real colour.
I think these are the only constraints required:
- optimise for smoothest curve (as before)
- XYZ coordinate of spectrum must equal input coordinate
- is bounded by 0-1.
- greatest possible luminance (I think this just means the max value of the spectrum should be 1)
Given a collection of points following those rules, some test would need to be done to verify that any linear combination of neighboring results also satisfies rules 2 and 3. Rule 1 doesn’t really have anything to satisfy since it’s just an optimisation, and I’m not sure about rule 4, but I’d imagine it would be close enough not to be an issue.
If this is going towards the mesh of presampled values idea, 3. should be true regardless, since you’d weigh rather than just straight up add them, whereas 2. is going to be really hard to satisfy exactly but could be made arbitrarily close given enough sample points. Maybe some adaptive approach could make sure enough density is present to make that work out to a given precision in challenging areas whereas easier areas would be more sparsely presampled.
I think 2 is also satisfiable by design of the XYZ colour space. Consider these two statements, I think it proves 2 will always be satisfied, but I’d have to check because I don’t trust my intuition on this.
A. Any two colours can be combined to form any colour along the line between their XYZ coordinates
B. The XYZ coordinate of a sum of spectra is equal to the sum of the individual XYZ coordinates of those spectra. (AKA You can either sum the spectra then convert to XYZ, or convert the spectra to XYZ then sum them, the result is the same)
By guess is that rule 1 and 4 will become less and less optimised the larger the distance is between the points. That’s where the tradeoff occurs.
Exactly. It’s a trivial adjustment to the view.
I would suggest not making any further plans beyond the spectral side simply because it’s very likely far too much in a single push, and starts over complicating things. UI is already a huge mountain to overcome, let alone introducing a new thing.
I would wager the best bet at this point is figure out a relatively flexible manner to pull spectral up samples from the existing RGB UI.
What primaries did you use? It would seem that they are conservative BT.709 as a guess? Wider primaries would illustrate the phenomena much better if that’s the case!
@briend and I have been kicking around spectral solving for too long now, and getting the primaries solver into Colour has been a goal. If you have an IM available, hit me via a PM and I’d be happy to try and step through it. I’m an oldschool type too, and Matlab still makes me lose me in the syntax, so the help would have to go the other way. I’m certainly no Python wizard, but even less of a MatLab wizard.
If you are talking about spectral adaptation over the army of adaption functions currently in Colour, Dr. Fairchild experimented with this back in 2007. The verdict was that further research had to be done. Largely because adaptation is psychophysical. There are more recent papers on Abney effect, and the possibility that the macular dyes form a six dimensional space with a degree of spectral sensitivity that might help to explain Abney, but again, it’s the “more research” case, so it’s hard to tell if it works well against the various predictive datasets.
All that said, it would be interesting to see how your tests went! Any chance you can do this with camera RGB as spectral sites, and upsample from a semi-solved, albeit artificial set of camera primaries?
Couldn’t agree more. None of this is going to be making it in to the early work, not until a well-established render and colour pipeline already exists.
Yeah this is with the unadapted rec.709 primaries. Though I’m not sure what phenomena you’re referring to, since what I was showing was that with a ‘fully saturated’ rec.709 light source, there’s still a spectrum of light there which means it can still illuminate ‘fully saturated’ materials. In master, a lamp only emitting green light will not have any impact on 100% red or blue diffuse materials. There are other phenomena which would become more apparent with wider primaries, which probably includes the one you’re thinking of.
Force your working reference to BT.2020 and try it. The transform back to BT.709 for display will be helluva ghastly without proper thought out gamut mapping, but your demonstration should be far more pronounced.
The Matlab code is this:
function rho=XYZ2rho(A,W,XYZw)
% Finds reconstructed reflectance (rho) from
% tristimulus values (XYZw) referenced to illum W,
% using "method 2" of (Burns SA. Numerical methods
% for smoothest reflectance reconstruction. Color
% Research & Application, Vol 45, No 1, 2020, pp 8-21.)
% A is the nx3 matrix of color matching functions.
% W is an nx1 illuminant vector, scaled arbitrarily.
% XYZw is a three element vector of illum-W-referenced
% tristimulus values in the 0 <= Y <= 1 convention range.
% rho is a nx1 vector of reflectances (or zeros if failure).
n=size(A,1);
D=full(gallery('tridiag',n,-2,4,-2));
D(1,1)=2; D(n,n)=2;
W_normalized=W/(A(:,2)'*W);
Aw=diag(W_normalized)*A;
rho=zeros(n,1); z=zeros(n,1); lambda=zeros(3,1);
count=0; maxit=20; ftol=1.0e-8;
while count <= maxit
r=exp(z); dr=diag(r); dra=dr*Aw; v=dra*lambda;
F=[D*z+v; Aw'*r-XYZw(:)];
J=[D+diag(v), dra; dra', zeros(3)];
delta=J\(-F); % solve system of equations J*delta = -F
z=z+delta(1:n);
lambda=lambda+delta(n+1:n+3);
if all(abs(F)<ftol)
rho=exp(z); return
end
count=count+1;
end
If I read this right, what the code does, step by step, is:
- given the matrix A of color matching functions with n spectral bins and three tristimulus values
- given a vector W of whitepoint illuminant W spectral data
- given a whitepoint XYZw with the XYZ coordinates corresponding to the illuminant W’s spectrum
- find how many bins there are, store it in n
- build a tridiagonal n by n matrix with 4 along the diagonal and -2 along the neighbouring diagonals. Call it D.
- Change the top left and bottom right elements of D to 2.
- Normalize W with respect to the color matching function of the Y-channel which is stored in A[:,2]. This is acomplished by dividing each component in W by dot(A[:,2],W)
- put W_normalized into the diagonal of a matrix and multiply by A to get Aw.
- initialize rho and z as zero vectors of length n.
- initialize lambda as a zero vector of length 3 (for the three primaries)
- initialize a counter variable count=0, an iteration limit maxint = 20, and an accuracy cutoff ftol = 1.e-8
- while count <= maxint:
– r is component-wise exp(z)
– dr is the diagonal matrix with r as its diagonal
– dra = dr * Aw
– v = dra * lambda
– F puts together two matrices on top of each other
— the top part of F is D * z + v
— the bottom part of F is transpose(Aw) * r - XYZw[:] (so a full copy of XYZw)
– J is built from four blocks:
— the top left block of J is D + diag(v)
— the top right block of J is dra
— the bottom left block of J is transpose(dra)
— the bottom right block of J is a 3x3 matrix of zeroes.
– delta is J multiplied by the inverse matrix of -F (this is the change between the previous and next iteration)
– z += delta[1:n]
– lambda += delta[n+1:n+3]
– if all(abs(F) < ftol) (so if the differences are small enough):
— calculate the vector rho = exp(z) (componentwise) and return it
– advance the counter count += 1 - return exp(z) (if it goes this path that means the error bound wasn’t met)
then rho is the vector of reflectances you’ve been looking for
I think numpy or scipy should have all necessary functions to pretty much translate this matlab code practically 1:1. I would probably factor out the max iteration count and accuracy as their own things though, rather than hardcoding them.
That being said, as far as I can tell this is actually the logarithmic method, not the hyperbolic tangent one. @Scott_Burns is that right? - If it makes little difference but the hyperbolic tangent version is algorithmically cheaper/better, shouldn’t we just use that?
Yes, only some minor comments:
“given a vector W of whitepoint illuminant W spectral data” W is the vector of the illuminant’s relative spectral power distribution. I generally think of the “white point” as being the tristimulus values we get from a perfect reflecting surface. Just a minor terminology thing.
“XYZw[:] (so a full copy of XYZw)” The colon acts to convert XYZ into a column vector, in case it was passed as a row vector instead.
“delta is J multiplied by the inverse matrix of -F” Matlab (and LAPACK) use a more advanced factoring method for solving linear equations that is more stable and reliable than premultiplication by the inverse of J, which is computationally expensive and prone to other performance problems.
Otherwise, you’ve got it!
You are also correct that this is the log version, not the hyperbolic tangent version. The log version can be applied to any color that has tristimulus values residing in the spectral locus. The h-t version requires that we are inside a subset of the spectral locus, i.e., the object color solid (colors arising from object reflectances bounded between 0 and 1). The log version can handle emissive sources, which is why I use it in the chromatic adaptation approach. (BTW, I’ve written Matlab functions that will test if a color is in the spectral locus or if it is in the object color solid.)
This probably belongs in a separate thread. Slap it up on a Colab and it should be easy to test and trial.
Yes, most of the chromatic adaptation transformations are “fine tuned” to match the experimental “corresponding colors” datasets. I agree with Fairchild that more experiments are needed to take into account other factors. But what’s really great about using smoothest spectral reconstruction to do adaptation is that it is independent of all of the experimental datasets and works from first principles, while outperforming the methods that are fine-tuned to the datasets, like Bradford, CAT02, and CAT16. Furthermore, all of those fine-tuned methods will go haywire as we move away from the central part of the spectral locus. For example, here is how CAT16 transforms colors on the boundary of the object solid (orange curve to green curve) when adapting from equal energy (orange dot) to an illuminant closer to the spectral locus (green dot):
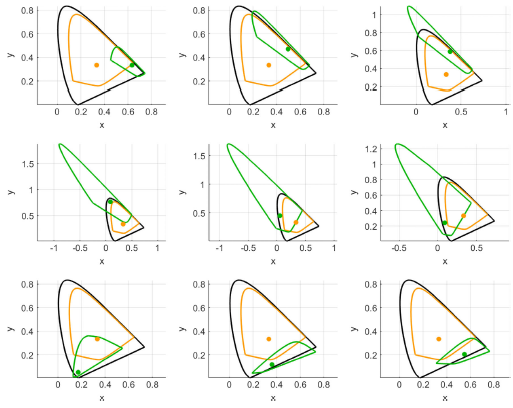
Many colors are ejected from the spectral locus, representing physically impossible colors. In contrast, here is the action of the spectral reconstruction approach:
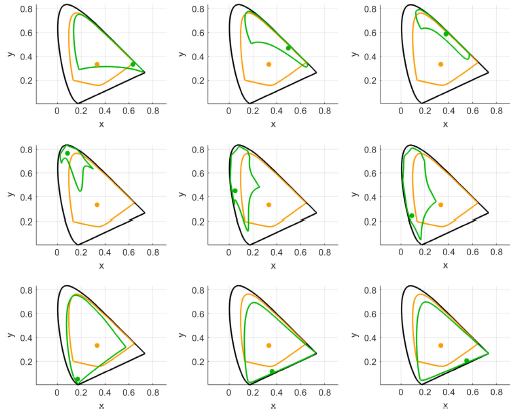
The adapted colors are always inside the spectral locus. (BTW, Bradford does even worse than CAT16 in this respect.)
I haven’t yet confirmed that it actually works (sorry, bit busy right now) but in principle this should be the translation of this code into python
(I copied the full collab and added the function “findprimaries()”. It is not yet used. I just verified that, at least, the interpreter doesn’t complain about syntax)
https://colab.research.google.com/drive/1i-73zvyvzPqEaoykNolddZFUpsz8MGq0
There is, afaik, a convention difference between matlab and Python in that matlab arrays start at 1. I adjusted the arrays accordingly. Hopefully that was correct like that.
@brecht I’ve started work on restructuring the throughput and PathRadiance etc to represent spectral data and I’m wondering what’s the most suitable way to do this - to me the accumulated light can contain contributions from multiple samples which means storing the contributions for each of the wavelengths isn’t right.
Is this understanding correct? Do the values in PathRadiance represent contributions accumulated over multiple samples, or only from a single sample? From looking at path_radiance_accum_sample it seems PathRadiances can be added together.
I’m also thinking of creating a new data type to represent an XYZ buffer, just to be more explicit about what the data represents, but I’m not familiar enough with C++ to know a good way to do that. Any ideas? What I’ve done initially is create a new struct and overridden all the relevant operators, but this seems very repetitive.
I’m not sure if I just need to learn more about C++, but it seems like making any changes to this area of the code requires huge rewrites. I’m wondering whether there’s the opportunity to reduce some complexity by containing the conversions which need to occur to one place, but I’m afraid in a system as large as Cycles, even getting to that point might be a pretty large undertaking.
Thanks for doing this @kram1032! I’m surprised to see so many python functions that parallel the Matlab ones. Now I just have to figure out how to run the code. Can I single-step through it and examine the content of variables during execution, like the debug function in Matlab?
VSCode has a great python debugger, you can copy the script and debug it following the instructions here. You can set breakpoints and inspect the values in variables.
Thanks @smilebags, I’ll check it out. Do you have a favorite reference to understand what a particular python statement does?
VSCode Intellisense does a pretty good job (F12 will navigate to a function definition which can help too), otherwise this probably covers most things.
https://docs.python.org/3/reference/
The first line of @kram1032’s code is n = length(cmfs). I went to the docs.python site and searched for “length”. Nothing in the 169 matches looks like any description of what that simple command does…