Recently, I’ve had to disabuse myself of the cherished belief that the equal sign (=) in Python just assigns a right hand value or reference to a left hand label. Depending on the prevailing environment, it can do more or do differently. In Blender, for left hand sides that expose RNA properties, = is adroitly overloaded; it is not a simple assignment operator.
# Let's make y-shear!
>>> yshear_mw
#~ Matrix(((1.0, 0.0, 0.0, 2.0),
#~ (0.25, 0.25, 0.0, 2.0),
#~ (0.0, 0.0, 0.125, 2.0),
#~ (0.0, 0.0, 0.0, 1.0)))
Expected:
>>> for k in range(-5, 6, 1):
yshear_mw @ Vector((k, 0, 0))
#~ Vector((-3.0, 0.75, 2.0))
#~ Vector((-2.0, 1.0, 2.0))
#~ Vector((-1.0, 1.25, 2.0))
#~ Vector((0.0, 1.5, 2.0))
#~ Vector((1.0, 1.75, 2.0))
#~ Vector((2.0, 2.0, 2.0))
#~ Vector((3.0, 2.25, 2.0))
#~ Vector((4.0, 2.5, 2.0))
#~ Vector((5.0, 2.75, 2.0))
#~ Vector((6.0, 3.0, 2.0))
#~ Vector((7.0, 3.25, 2.0))
That is, for input geometry, points equally spaced on the x-axis:
- Data translates x = +2, y = +2, z= +2
- Step along x: +1.00
- Step along y: +0.25, shear component
- No step apparent along z as input points showed no z-ward displacement and there is no shear component along z.
All is well. Let’s assign:
>>> bpy.data.objects['Child'].matrix_world = yshear_mw
>>> bpy.data.objects['Child'].matrix_world
#~ Matrix(((1.023111343383789, -0.030431389808654785, 0.0, 2.0),
#~ (0.125471830368042, 0.24814094603061676, 0.0, 2.0),
#~ (0.0, 0.0, 0.125, 2.0),
#~ (0.0, 0.0, 0.0, 1.0)))
#~
Ah me. Not the same matrix. Spot check. Compare with above:
>>> bpy.data.objects['Child'].matrix_world @ Vector((-5, 0, 0))
#~ Vector((-3.1155567169189453, 1.37264084815979, 2.0))
>>> bpy.data.objects['Child'].matrix_world @ Vector(( 5, 0, 0))
#~ Vector((7.115556716918945, 2.62735915184021, 2.0))
Not even close. What happened?
TL;DR: = won’t always do what you think it will do.
Tell me more: = can be overloaded in certain environments. In the Blender Python API, it is overloaded in such a way so that when some attempt is made to change the RNA property matrix_world on an object, other parts of the object related to UI-oriented gets() and sets(), representing rotations, translations and scalings, are bought into line with the proposed transform. That pipeline is optimized along a simplified decomposition scheme that accommodates rotations, scalings and translations. It executes very quickly, keeping UI framerates decently quick. But some kinds of matrices - like shears - don’t fit the simplified decomposition scheme and data are lost.
This lost is manifested in matrix assignments that don’t seem to assign as expected.
Rainy Day Reading: To get a sense of what happens in that deceptively simple seeming = assignment:
- Take a debug-built Blender running under GNU’s
gdb or some other IDE.
- Run Blender itself with an addon that (at least) creates a
new mesh object and tries to position it by setting matrix_world.
- Put
pdb tripwires - pdb.set_trace() - just before the naïve matrix_world assignment.
- On gnu debugger side, breakpoints have been set in select functions.
See commentary for particulars.
Dropping into Python just after pdb.set_trace() pdb prompts are (Pdb), GNU prompts are (gdb).
> /home/gosgood/.config/blender/2.93/scripts/addons/kkut/__init__.py(273)execute()
-> ob.matrix_world = Matrix(yshear_mw)
(Pdb) ob.name
'Child_loop'
Stepping past the Python-level assignment:
(Pdb) n
[Switching to Thread 0x7fffe5646640 (LWP 13542)]
Thread 1 "blender" hit Breakpoint 1, rna_Object_internal_update(UNUSED_bmain=0x7fff8583a038, UNUSED_scene=0x7fffce3b9438, ptr=0x7fff82c2aa10) at /home/gosgood/git_repositories/blender/source/blender/makesrna/intern/rna_object.c:332
332 DEG_id_tag_update(ptr->owner_id, ID_RECALC_TRANSFORM);
(gdb) c
(Very) roughly, rna_Object_internal_update(Main *bmain, Scene *scene, PointerRNA *ptr) takes the matrix on the right hand side of the Python-level assignment and sets the following object fields as needed:
ob->loc,ob->scale,ob->rot
That’s phase one. Laying groundwork for phase two, rna_Object_internal_update() also tags Child_loop for downstream depsgraph re-evaluation. That deferred activity takes these three object fields as inputs and rebuilds afresh ob->obmat, from which properties matrix_basis and matrix_world derive.
Hit ‘continue’ at gdb level. At Python level, single-stepping through the script following the assignment…
> /home/gosgood/.config/blender/2.93/scripts/addons/kkut/__init__.py(274)execute()
-> bpy.context.view_layer.active_layer_collection.collection.objects.link(ob)
(Pdb) n
> /home/gosgood/.config/blender/2.93/scripts/addons/kkut/__init__.py(295)execute()
-> if lclmode == 'EDIT' :
(Pdb) n
> /home/gosgood/.config/blender/2.93/scripts/addons/kkut/__init__.py(296)execute()
-> bpy.ops.object.editmode_toggle()
(Pdb) n
Ding! Toggling edit mode kicks off the aforementioned depsgraph re-evaluation.
(gdb) p ob->id.name
$1 = "OBChild_loop", '\000' <repeats 53 times>
Behind the curtain, depsgraph evaluation generates the matrix_basis RNA object property from the enumerated object fields listed above. It is the first part of that quick, simplified synthesis scheme that optimizes for scalings, rotations and translations, but cannot generally synthesize all types of matrices.
Rather than the literal gdb step-through - a bit long and tedious - here’s a list in order of visitation:
-
BKE_object_eval_local_transform(Depsgraph *depsgraph, Object *ob)
a. BKE_object_to_mat4(Object *ob, float r_mat[4][4])
I. BKE_object_to_mat3(Object *ob, float r_mat[3][3])
i. BKE_object_scale_to_mat3(Object *ob, float mat[3][3])
ii. BKE_object_rot_to_mat3(const Object *ob, float mat[3][3], bool use_drot)
b. After scaling and rotation, translation is handled at the tail end of BKE_object_to_mat4(): add_v3_v3v3(r_mat[3], ob->loc, ob->dloc);
-
If an object is parented (ob->parent is populated) matrix_basis is composited with parent object transforms, leading to matrix_world: BKE_object_eval_parent(Depsgraph *depsgraph, Object *ob). Otherwise, matrix_basis == matrix_world
-
Cleanup: BKE_object_eval_transform_final(Depsgraph *depsgraph, Object *ob\)
That is what follows, direct and deferred, from a ‘simple’ assignment to matrix_world at the Python level.
Well, there is the Shear tool….
Perhaps you would prefer not to change the mesh itself, favoring object-level transform. Or you have a more general case: an exotic matrix of some sort that is known to be mangled, given reasons above, on assignment to matrix_world.
In that case, Singular Value Decomposition to the rescue. Also spend a rainy day with Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), “Section 2.6”, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press.
Lets work out a practical example using a simple y shear (from Blender Python console):
>>> import numpy as np
>>>
>>> yshear = np.identity(3)
>>> yshear[1,0] = 3.0
>>> yshear
array([[1., 0., 0.],
[3., 1., 0.],
[0., 0., 1.]])
The game is to use SVD to re-express yshear as a composition of three matrices: U a ‘pure’ rotation (no scaling), S, a ‘pure’ scaling (no rotation) and VH, another ‘pure’ rotation. Being ‘pure’ rotations and scalings, these components can individually glide through Blender without difficulty, while the composite shear gets mangled. See the nice diagram accompanying the Wikipedia article.
My ‘SVD’ pipeline only needs to solve for the 3 x 3 upper-left submatrix of the full-bore 4 x 4 homogeneous matrix, the rotation and scaling part. I’ll add the translation component post-SVD.
>>> u, s, vh = np.linalg.svd(yshear)
>>> u
array([[-0.28978415, 0. , -0.95709203],
[-0.95709203, 0. , 0.28978415],
[ 0. , 1. , 0. ]])
>>> s
array([3.30277564, 1. , 0.30277564])
>>> vh
array([[-0.95709203, -0.28978415, -0. ],
[ 0. , 0. , 1. ],
[-0.28978415, 0.95709203, 0. ]])
Unlike the other two 3 x 3 rotation matrices, s is a simple vector containing the singular values diagonal.
Repackaging to homogeneous matrices entail setting the upper 3x3 quadrant of 4x4 identity matrices, to wit:
# XXX XXX0
# XXX --> XXX0
# XXX XXX0
# 0001
mu = np.identity(4)
ms = np.identity(4)
mvh = np.identity(4)
THREE = slice(None,-1, 1)
mu[THREE,THREE] = u
ms[THREE,THREE] = np.diag(s, 0)
mvh[THREE,THREE] = vh
As @Hadriscus suggests, the game continues with setting the matrix_world properties of three Empty parents, then parenting the mesh object to the last Empty on the chain. The flavor of parenting to use is Object (without inverse) so that the objects on the chain immediately reposition in response to parenting, without Blender generating the compensatory inverse matrix.
Off camera, create Empties MU, MS, MVH equivalents mu, ms, mvh
You now should be able to do something like this:
>>> bpy.data.objects['MU'].matrix_world = Matrix(mu)
>>> bpy.data.objects['MS'].matrix_world = Matrix(ms)
>>> bpy.data.objects['MVH'].matrix_world = Matrix(mvh)
>>>
>>> bpy.data.objects['MU'].matrix_world
#~ Matrix(((-0.28978410363197327, -4.1835821917857174e-08, -0.9570920467376709, 0.0),
#~ (-0.9570920467376709, 1.2666866666677379e-08, 0.28978410363197327, 0.0),
#~ (0.0, 1.0, -4.371138828673793e-08, 0.0),
#~ (0.0, 0.0, 0.0, 1.0)))
#~
>>>
>>> bpy.data.objects['MS'].matrix_world
#~ Matrix(((3.3027756214141846, 0.0, 0.0, 0.0),
#~ (0.0, 1.0, 0.0, 0.0),
#~ (0.0, 0.0, 0.30277565121650696, 0.0),
#~ (0.0, 0.0, 0.0, 1.0)))
>>>
>>> bpy.data.objects['MVH'].matrix_world
#~ Matrix(((-0.9570920467376709, -0.28978410363197327, -1.2666865778498959e-08, 0.0),
#~ (0.0, -4.371138828673793e-08, 1.0, 0.0),
#~ (-0.28978410363197327, 0.9570920467376709, 4.1835821917857174e-08, 0.0),
#~ (0.0, 0.0, 0.0, 1.0)))
#~
>>>
Rounding errors introduce noise on the order of 1.0e-07, but apart from that, the matrix_world’s generally reproduce the components garnered from SVD, unmangled.
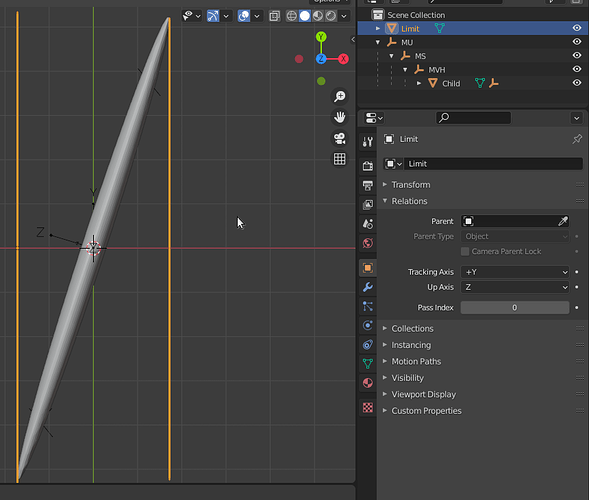
The game concludes with the parenting (without inverse):
MS to MU - the unparented rootMVH to MSChild to MVH - See the screen shot
This is a top view, peering down +Z to the origin. Limit brackets at the original unsheared geometry width, this to convince myself that I was obtaining a shear and not a sneaky rotation.
A PITA? You bet, there is no end to assigning the wrong matrix to the wrong Empty or parenting out of order. For shearing, the Shear tool invites. For other exotics, consider this approach, as SVD is a
general purpose matrix deconstructor. I suppose one could make a small library of these exotic transformation parenting chains for quick deployment.
Sorry for the length; hope this is a help.