Curve Connect Node Development

Archive Geometry Nodes
1

I’ve been working on ways to make a “Connect Curve” node work. I’ve run into a couple of dead ends and wanted to share the thought process that has gotten me this far.

There are 2 modes for the node: Order and Threshold

Order is an easy one. Simply go through the splines in the order that they exist in the input geometry. Add them to a “merge map” structure that can be passed to an output curve building function.

Threshold is where I have run into trouble.

The first idea went like this:

  • Input a threshold distance
  • Create a flattened list of all of the splines
  • Build a list of all “endpoints” (start and end)
  • Create a KD tree of the endpoints of all of the splines
  • Start on the first curve of the geometry and add it to the output curve, mark it as processed in the spline list and add it to the merge map
  • Using the KD tree, look up the closest endpoint from another spline within the threshold
  • If that spline has not been processed add it to the output curve, mark it as processed and add it to the merge map. then repeat the last step
  • If it has been processed, skip it until an unprocessed spline is found and repeat from there. If none are found, the output curve spline is ended and a new spline is created with the next available unprocessed spline on the merge map.
  • continue until all splines are processed.
  • pass the merge map to the curve output function

For the most part, this implemented pretty well, but ran into an artistic issue:

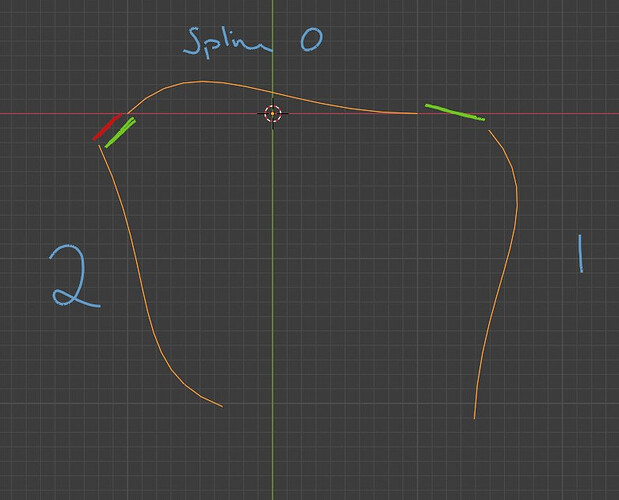
image
image782×631 70.4 KB

This algorithm would produce the red connection in this image. Since spline 0 would match to spline 2, but when spline 1 is processed, it would not connect to spline 0 since spline 0 was already “used”. I believe this is mainly because while it is based on distance, this algorithm is still very much a linear search. So later closer connections may not be found until it is too late to use them.

A second algorithm that I attempted to implement to address this issue was this:

  • Create a flattened list of splines for lookup purposes
  • Build a list of all endpoints
  • Build a KD Tree of all of the endpoints
  • Go through each endpoint and use the KD tree to make a list of all of the endpoints connection permutations within the threshold, sorted by distance smallest to largest. Deduplicting for reverse relationships (endpoint 1=>5 is the same as 5=>1)
  • Use this ordered list of connections to determine the order the splines should be added to the merge map - (This is where I had trouble managing how to build this correctly. It seems that all of the data needed is there, it was more a matter of how to manage it.)
  • Pass the merge map to the output curve function.
5 Likes
2

Hmm, getting a proper solution to this isn’t trivial, is it! Doing a bit of research, I think this is actually a common problem: Closest pair of points problem - Wikipedia

Maybe that’s helpful? The distance threshold could be an important optimization, like you mention though.

3

The KD tree made getting the pairs a lot easier. even getting them down to a distance-ordered list of endpoint pairs wasn’t too bad. It’s distilling that information into the list of splines in the right order and reversing them when the case requires is my real hurdle.

4

Not 100% sure, but I think flexi bezier tools addon can do this? Maybe worth checking out.

5

Though I have not a 99% definite answer on how to roll with this, I can think of this strategy.

  1. You always have to start from the active curve, active curve will act as an initiator that will make things much easier in some ways. Such as for example if you select all but mark the curve [#1] manually as active (explicit selection) then you immediately will know the order of starting.
    As for example Blender uses this pattern quite a lot, most notable is Grid Fill, where you will have to explicitly mark the corner as active to get a perfect result at once, otherwise if you go by chance you will end up tuning the steps randomly until you get a good match.

  2. Once you have the curve #1 selected, you can start a flood fill to check for connections.

  3. Once you have figured out the chain of connections, you will have to flip curves that are reversed, have only one flow from start to the end.

  4. You will be able now to fix the positions of the curves now.

P.S. I had to solve such a similar problem (except setting the positions - they were snapped manually from the user). See if is helpful.

Sorting the curves? - #2 by grosgood