Hi
I’m new to Blander but I want to use it to edit various stl file via Python code. I have gotten started with making some primatives, transforming them and subtracting them. Here is the code:
import bpy
import math as m
bpy.ops.mesh.primitive_cube_add(enter_editmode=False, align='WORLD', location=(0, 0, 0), scale=(1,1,1))
bpy.ops.mesh.primitive_cone_add(enter_editmode=False, align='WORLD', location=(0, 0, 0.5), scale=(1,1,1))
cube = bpy.data.objects['Cube']
cube.location.x -= 1
cube.rotation_euler[0] += m.radians(45)
cone = bpy.data.objects['Cone']
bool_one = cube.modifiers.new(type="BOOLEAN", name="bool 1") # create and store a modifier
bool_one.object = cone
bool_one.operation = 'DIFFERENCE'
cone.hide_viewport = True
Material stuff
Now would like to change the color of individual facets of the mesh depending on their orientation in space. Below is some nonfunctional code to illustrate my problem. There are currently two issues:
-
I can’t assign material to a single facet.
-
The normal vector is given in local coordinates and I want them in world space.
material_hang = bpy.data.materials[3]
#cube.active_material = material_hang # This works!
for fac in cube.data.polygons:
if fac.Normal * (0,0,1) > 0:
fac.ChangeColorYou(Red)
Material stuff
Whenever I wish to know how well one vector - such as face normals -
aligns with another I reach for the dot product; the function is built
into Blender’s Vector. The scalar value which the dot product
gives may be employed as an ‘alignment meter’. 1: two normalized
vectors are colinear and pointing in the same direction. -1: two
normalized vectors are colinear, but pointing in opposite directions.
(-1.0, … 1.0): the two vectors define a plane, the alignment meter
returns the cosine of the angle separating them in that plane. Note:
the parenthetical notation means “open set” - everything between negative
and positive one are in the set, but neither of the limit values are. While I have
been particular about “normalized” vectors - those whose lengths are
one - if I forget to normalize vectors and still take dot products
then I don’t get the cosine; I get a scaled version of it. That
version varies in the same manner; it’s a ‘relative alignment meter’
For most purposes that works and it cuts down on the math, so it is
faster to compute.
I think the simplest approach to your problem is to dispense
with Python entirely, and define a material that incorporates
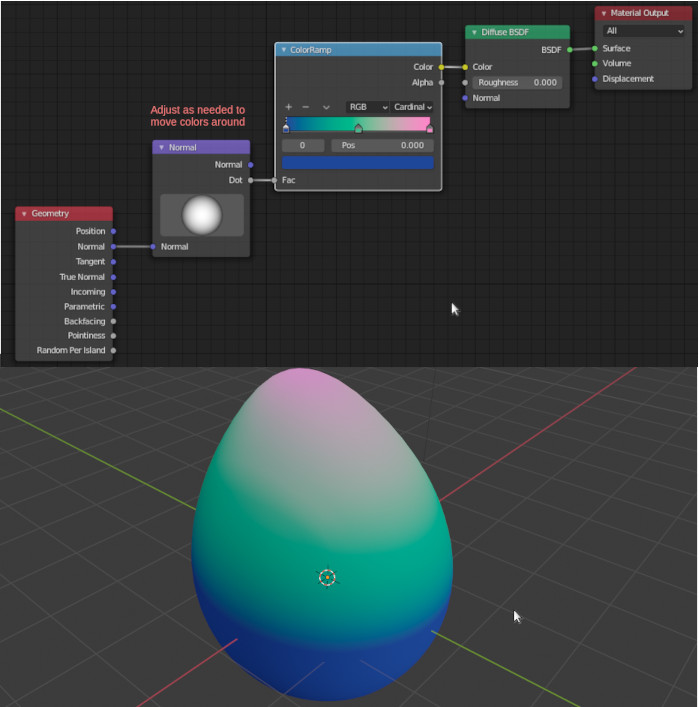
an alignment meter. Here is one (version 2.90) possibility:
Now the material automagically assigns each face a color based on its orientation with respect
to the Normal node. You may vary the Normal node to suite your needs and change
ColorRamp as you see fit.
The Normal node is newish. In older blenders, use Combine XYZ to input
vectors by hand numerically and combine that input with the Normal input from
the Geometry node by way of the Vector Math node, which contains the dot product.
Though this, being the python section, then I best include some Python,
else the board moderators might descend upon me in a white
heat. Here are some fragments that might be useful here and there:
import bpy
from bpy import data as D
from bpy import context as C
from mathutils import *
from math import *
# WARNING: Illustrations. No error checking! Little sanity checking!
# Fetch the active object
aod = bpy.context.active_object.data
# Make a list of tuples. tuple[0]: face index; tuple[1]: dot product
# "awz" == Align With Zed
awz = [(f.index, f.normal.dot(Vector((0, 0, 1)))) for f in aod.polygons]
# This is how well the 32nd face aligns with up:
# i. e., dot product is negative: The face normal points downward, more-or-less
awz[32]
#~ (32, -0.6394280791282654)
# Associate per-face upward alignment as a polygon property.
# "AWZ" == "Align With Zed"
# Run this code while the 'Cube' is in object mode
aod.polygon_layers_float.new(name = 'AWZ')
#~ bpy.data.meshes['Cube'].polygon_float_layers["AWZ"]
# Sanity check:
aod.polygon_layers_float.keys()
#~ ['AWZ']
for face in aod.polygons :
aod.polygon_layers_float['AWZ'].data[face.index].value = face.normal.dot(Vector((0.0, 0.0, 1.0)))
# Face 0 points rather downward.
aod.polygon_layers_float['AWZ'].data[0].value
#~ -0.5794727206230164
# Face 1598 is almost at right-angles with up
aod.polygon_layers_float['AWZ'].data[1598].value
#~ 0.0010248979087918997
# You may make as many float layers as you like;
# give them unique names. There are also boolean,
# integer and byte array layers as well, but the
# byte array is currently broken; fixing it is a
# long term to-do.