Bpy.ops.transform.rotate, option 'axis'

Archive Python API
1

Hello.

In 2.79, I used this nice operator with which I could turn an object (e.g., camera) around a vector (here, e.g., axis = object_camera_vec).

bpy.ops.transform.rotate(value=(90.02pi/360.0),
axis=object_camera_vec,
orient_matrix=camera.rotation_euler,
constraint_axis=(False, False, False),
orient_type=‘GLOBAL’,
mirror=False, proportional=‘DISABLED’,
proportional_edit_falloff=‘SMOOTH’,
proportional_size=1, snap=False,
snap_target=‘CLOSEST’, snap_point=(0, 0, 0),
snap_align=False, snap_normal=(0, 0, 0),
release_confirm=False)

This option ‘axis’ does not exist anymore in 2.80. I found the following in the API description for 2.80:

bpy.ops.transform. bend ( value=(0.0) , mirror=False , proportional=‘DISABLED’ , proportional_edit_falloff=‘SMOOTH’ , proportional_size=1.0 , snap=False , snap_target=‘CLOSEST’ , snap_point=(0.0 , 0.0 , 0.0) , snap_align=False , snap_normal=(0.0 , 0.0 , 0.0) , gpencil_strokes=False , center_override=(0.0 , 0.0 , 0.0) , release_confirm=False , use_accurate=False )

So, what now? What replaces this ‘axis’ option?

Thanks in advance for some comments.

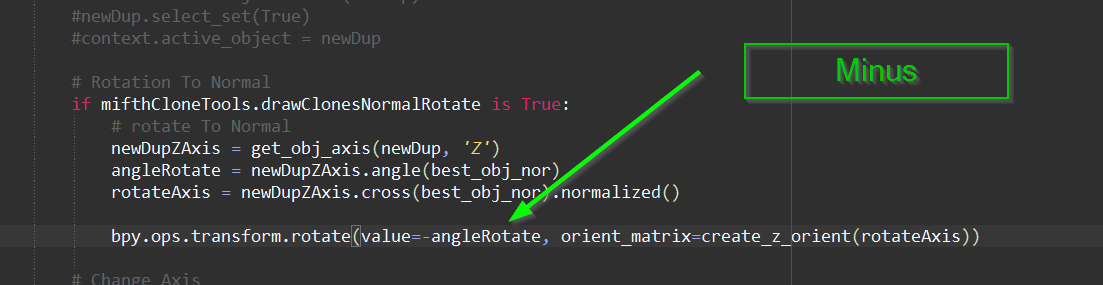
EDIT: Please, forget this operator above, I meant this one here:>

bpy.ops.transform. rotate ( value=0.0 , orient_axis=‘Z’ , orient_type=‘GLOBAL’ , orient_matrix=((0.0 , 0.0 , 0.0) , (0.0 , 0.0 , 0.0) , (0.0 , 0.0 , 0.0)) , orient_matrix_type=‘GLOBAL’ , constraint_axis=(False , False , False) , mirror=False , proportional=‘DISABLED’ , proportional_edit_falloff=‘SMOOTH’ , proportional_size=1.0 , snap=False , snap_target=‘CLOSEST’ , snap_point=(0.0 , 0.0 , 0.0) , snap_align=False , snap_normal=(0.0 , 0.0 , 0.0) , gpencil_strokes=False , center_override=(0.0 , 0.0 , 0.0) , release_confirm=False , use_accurate=False )

2

Why are you comparing rotate() and bend()?

bpy.ops.transform.rotate(value=0, orient_axis='Z', orient_type='GLOBAL', orient_matrix=((0, 0, 0), (0, 0, 0), (0, 0, 0)), orient_matrix_type='GLOBAL', constraint_axis=(False, False, False), mirror=False, proportional='DISABLED', proportional_edit_falloff='SMOOTH', proportional_size=1, snap=False, snap_target='CLOSEST', snap_point=(0, 0, 0), snap_align=False, snap_normal=(0, 0, 0), gpencil_strokes=False, center_override=(0, 0, 0), release_confirm=False, use_accurate=False)

Check orient_axis and orient_matrix.

3

OMG, MACHIN3, right! It probably was too late yesterday … :sunglasses:

What I meant was:

bpy.ops.transform. rotate ( value=0.0 , orient_axis=‘Z’ , orient_type=‘GLOBAL’ , orient_matrix=((0.0 , 0.0 , 0.0) , (0.0 , 0.0 , 0.0) , (0.0 , 0.0 , 0.0)) , orient_matrix_type=‘GLOBAL’ , constraint_axis=(False , False , False) , mirror=False , proportional=‘DISABLED’ , proportional_edit_falloff=‘SMOOTH’ , proportional_size=1.0 , snap=False , snap_target=‘CLOSEST’ , snap_point=(0.0 , 0.0 , 0.0) , snap_align=False , snap_normal=(0.0 , 0.0 , 0.0) , gpencil_strokes=False , center_override=(0.0 , 0.0 , 0.0) , release_confirm=False , use_accurate=False )

From Link

4

Dear all.

I found a solution, thanks to the description from here:

import bpy
from math import radians
from mathutils import Matrix

# we will demonstrate on an active object
obj = bpy.context.active_object

def rotate_object(rot_mat):
    # decompose world_matrix's components, and from them assemble 4x4 matrices
    orig_loc, orig_rot, orig_scale = obj.matrix_world.decompose()
    #
    orig_loc_mat   = Matrix.Translation(orig_loc)
    orig_rot_mat   = orig_rot.to_matrix().to_4x4()
    orig_scale_mat = (Matrix.Scale(orig_scale[0],4,(1,0,0)) @ 
                      Matrix.Scale(orig_scale[1],4,(0,1,0)) @ 
                      Matrix.Scale(orig_scale[2],4,(0,0,1)))
    #
    # assemble the new matrix
    obj.matrix_world = orig_loc_mat @ rot_mat @ orig_rot_mat @ orig_scale_mat 

# rotation here: 45°
# you can also use as axis 'Y' or 'Z', or a custom vector like (x,y,z)
rotate_object( Matrix.Rotation(45, 4, 'X') )

Just put an object inside the viewer and execute this in the scripting window.

1 Like
5

Minor correction to Blenderphys’ script:
This line:
rotate_object( Matrix.Rotation(45, 4, 'X') )
Should be this:
rotate_object( Matrix.Rotation(radians(45), 4, 'X') )

Though if all you are doing is a 45 degree rotation on the ‘X’ axis (unless I’m misunderstanding something), I think you might be able to get away with just this:

import bpy
from math import radians
from mathutils import Matrix

obj = bpy.context.active_object
obj.matrix_world @= Matrix.Rotation(radians(45), 4, 'X')
1 Like
6

Anyone have a working example of how to do an arbitrary axis rotation around a fixed point (not an object’s origin) with the updated `bpy.ops.transform.rotate’ for 2.80? For 2.79 I could do something like this:

from copy import deepcopy
from math import degrees, radians, pi
import bpy
from mathutils import geometry, Euler, Matrix, Quaternion, Vector

v3d = [s for a in bpy.context.screen.areas if a.type == 'VIEW_3D'
  for s in a.spaces if s.type == 'VIEW_3D']
if len(v3d) == 0:
  print("Error, could not find VIEW_3D in visible editors.")
else:  # delete everything and add a plane
  bpy.ops.object.select_all(action='SELECT')
  bpy.ops.object.delete(use_global=False)
  bpy.ops.mesh.primitive_plane_add(view_align=False, enter_editmode=False, 
    location=(2, 1, 2), rotation=(radians(90), 0, 0))
  bpy.ops.object.transform_apply(location=False, rotation=True, scale=False)

  pivot_co = Vector((2.0, 2.0, 2.0))
  rot_angle = radians(-20)
  rot_axis = Vector((0.0, -0.7071067690849304, -0.7071067690849304))

  piv_back = deepcopy(v3d[0].pivot_point)
  v3d[0].pivot_point = 'CURSOR'
  curs_loc_back = bpy.context.scene.cursor_location.copy()
  bpy.context.scene.cursor_location = pivot_co.copy()

  bpy.ops.transform.rotate(value=rot_angle, axis=rot_axis,
    constraint_axis=(False, False, False))

  bpy.context.scene.cursor_location = curs_loc_back.copy()
  v3d[0] = deepcopy(piv_back)
  print(bpy.context.active_object.matrix_world)

The plane created by the script has this for its matrix_world attribute before the rotation (bpy.ops.transform.rotate)

<Matrix 4x4 (1.0000, 0.0000, 0.0000, 2.0000)
            (0.0000, 1.0000, 0.0000, 1.0000)
            (0.0000, 0.0000, 1.0000, 2.0000)
            (0.0000, 0.0000, 0.0000, 1.0000)>

After the rotation, the plane has this for its matrix_world attribute:

<Matrix 4x4 ( 0.9397, -0.2418, 0.2418, 2.0),
            ( 0.2418,  0.9698, 0.0302, 1.0),
            (-0.2418,  0.0302, 0.9698, 2.0),
            ( 0.0,     0.0,    0.0,    1.0)))

I have been trying to tweak the above script to get the same result in 2.80, but have not had any luck. I’ve done this “manually” with Python before (rotating each selected item one at a time using matrices or quaternions), but that often resulted in a huge performance hit when a large amount of geometry was being transformed :frowning:

This is what I have come up with so far for 2.80:

from math import degrees, radians, pi
import bpy
from mathutils import geometry, Euler, Matrix, Quaternion, Vector

# delete everything and add a plane
bpy.ops.object.select_all(action='SELECT')
bpy.ops.object.delete(use_global=False)
bpy.ops.mesh.primitive_plane_add(view_align=False, enter_editmode=False, 
  location=(2, 1, 2), rotation=(radians(90), 0, 0))
bpy.ops.object.transform_apply(location=False, rotation=True, scale=False)

pivot_co = Vector((2.0, 2.0, 2.0))
rot_angle = radians(-20)
rot_axis = Vector((0.0, -0.7071067690849304, -0.7071067690849304))

bpy.ops.transform.rotate(value=rot_angle, center_override=pivot_co,
  constraint_axis=(False, False, False))

print(bpy.context.active_object.matrix_world)

This 2.80 script results in the plane having this for its matrix_world attribute after bpy.ops.transform.rotate

<Matrix 4x4 (0.9698,  0.0302, -0.2418, 1.9698)
            (0.0302,  0.9698,  0.2418, 1.0302)
            (0.2418, -0.2418,  0.9397, 2.2418)
            (0.0000,  0.0000,  0.0000, 1.0000)>

Which (even without making use of rot_axis) still has mostly the same values as the 2.79 script (post rotation), but in a different order.

7

@ideasman42 It looks like it was this commit you did back in February that removed the “axis” option that allowed for entering a Vector with an arbitrary axis into a transform.rotate call:
6ebad22091c06f1e11e5efca7f19b1800e91fe09

Is it still possible to do arbitrary axis rotations around a non-origin point with the updated transform.rotate code or is this option gone for good? The only way I can see to do this now is using some ugly and complex hacks to the viewport camera.

8

Set the orient_matrix, then set the orient_axis to the axis of the matrix you want to use.

For a view rotation the oritent_matrix is set to the view matrix, rotating around the Z axis.

9

I was able to come up with a function to generate a 3x3 matrix from the vector you would plug into the older axis option from 2.79’s transform.rotate. You then enter the matrix this function returns into 2.80’s orient_matrix option and set the orient_axis equal to 'Z' in the updated transform.rotate syntax and it should work the same as it did in 2.79. My function below is based off of this function in Animation Nodes.

from math import isclose
from mathutils import Matrix, Vector

def create_z_orient(rot_vec):
    x_dir_p = Vector(( 1.0,  0.0,  0.0))
    y_dir_p = Vector(( 0.0,  1.0,  0.0))
    z_dir_p = Vector(( 0.0,  0.0,  1.0))
    tol = 0.001
    rx, ry, rz = rot_vec
    if isclose(rx, 0.0, abs_tol=tol) and isclose(ry, 0.0, abs_tol=tol):
        if isclose(rz, 0.0, abs_tol=tol) or isclose(rz, 1.0, abs_tol=tol):
            return Matrix((x_dir_p, y_dir_p, z_dir_p))  # 3x3 identity
    new_z = rot_vec.copy()  # rot_vec already normalized
    new_y = new_z.cross(z_dir_p)
    new_y_eq_0_0_0 = True
    for v in new_y:
        if not isclose(v, 0.0, abs_tol=tol):
            new_y_eq_0_0_0 = False
            break
    if new_y_eq_0_0_0:
        new_y = y_dir_p
    new_x = new_y.cross(new_z)
    new_x.normalize()
    new_y.normalize()
    return Matrix(((new_x.x, new_y.x, new_z.x),
                   (new_x.y, new_y.y, new_z.y),
                   (new_x.z, new_y.z, new_z.z)))
1 Like
10

Hi @_nBurn ,
Thank you for your code. I used it for a DrawClones tool as 2.7 worked differently. But I found a bug where my tool works incorrectly with 2.90+. I reported it here https://developer.blender.org/T85734

11

For an update on this issue from the discussion on the blender developer site, bpy.ops.transform.rotate now requires an axis constraint in the constraint_axis argument. To place an axis constraint on the 'Z' axis you would use:
constraint_axis=(False, False, True)

Example usage:

    o_mat = create_z_orient(rot_axis)
    bpy.ops.transform.rotate(
            value=rot_angle, 
            orient_axis='Z',
            orient_matrix=o_mat,
            center_override=Vector(pivot_pt),
            constraint_axis=(False, False, True),
            use_accurate=True
            )

This should fix the unexpected results when rotating about an arbitrary axis in Blender 2.93. This will not fix rotations for the official Blender 2.92.0 release though. It doesn’t appear it’s possible to do arbitrary axis rotations using bpy.ops.transform.rotate in 2.92.0 and it also does not appear the Blender Foundation will be releasing a bugfix “2.92.1” release either.

A possible workaround for 2.92.0 would be to use Blender’s mathutils module to calculate an updated matrix_world value for the object you are doing the arbitrary axis rotation on. Maybe something like this:

import math
from mathutils import Matrix, Vector

mat_world_beg = Matrix((
   ( 0.9330, -0.3536, -0.0670,  1.7804),
   ( 0.3536,  0.8660,  0.3536,  2.1589),
   (-0.0670, -0.3536,  0.9330,  0.7804),
   ( 0.0000,  0.0000,  0.0000,  1.0000)
))
pivot_pt = Vector(( 2.2928,  3.7321,  1.2928))
rot_axis = Vector(( 0.0670, -0.3536, -0.9330))
rot_angle = math.radians(-40)
mat_rot = Matrix.Rotation(rot_angle, 4, rot_axis)
pivot_pt_rot = mat_rot @ pivot_pt
pivot_pt_diff = pivot_pt - pivot_pt_rot
transl_mat = Matrix.Translation(pivot_pt_diff)
mat_result = transl_mat @ mat_rot @ mat_world_beg

print("mat_result:")
print(mat_result)
'''
<Matrix 4x4 ( 0.4874, -0.8706, -0.0670, 2.7430)
            ( 0.8275,  0.4361,  0.3536, 2.1149)
            (-0.2786, -0.2278,  0.9330, 0.8662)
            ( 0.0000,  0.0000,  0.0000, 1.0000)>
'''
1 Like
12

Hi @_nBurn ,
It looks like this code works correctly. All I had to do is to negate an angle.

image
image1103×285 21.3 KB

image
image1129×962 118 KB

My code is in the MifthTools addon:

1 Like