I rendered an alternate version to this jade in a different lighting condition. Still all blackbody light sources though.
Believe it or not, as “simple” as this seems, it is an exceptionally difficult problem to solve. That is, all of what we use is based around the CIE XYZ model for going to and from colour spaces. While it’s useful for this to an extent, it is also based around linear algebra.
Why is this somewhat problematic? Because if we do a gamut map using a brute force 3x3, the question can be asked of meaning. If we change primaries from one to the other, we aren’t really faced with an easy way to gamut map the intention of the spectra to the output context. That’s the whole nasty rabbit hole of gamut mapping, all over again, and why there isn’t something in place yet.
That’s mostly on me, so I apologize. It’s a hell of a tricky thing to solve once you get into the weeds. If we gamut clip the result, no one will have any idea what the hell they are looking at, and if we compress the results toward the achromatic axis, that too is demonstrably wrong. Just no easy solutions here!
It stinks. It’s really challenging to get right.
There is hope though, and I’m hopeful the current bit of experimenting will give something useful.
It would be great to have the fully functional version and I’m really looking forward to what you come up with.
However, since I don’t have a Filmic Spectral or wide gamut rendering or anything like that for now anyway, I’d just need it to work for sRGB without anything fancy for now. I’d only actually compare renders with the sRGB standard scene transform.
See above. To the best of my knowledge and understanding, it cannot be achieved. Every single option is woeful in a majority of capacities.
Right, I believe we’re saying the same thing, as that’s precisely what I described in my last paragraph. I was trying to describe it in a way that people who don’t know what e.g. “metamer” or “color observer” means would still grasp the idea.
I think you’re coming at it from a perceptual perspective (e.g. you can perceptually invert it, relative to the particular color observer), whereas I’m coming at it from a spectral perspective (you can’t actually invert it to get back the original spectrum).
I mean, again, it depends on your perspective. From a perceptual perspective, when working with a set of sufficiently similar color observers (e.g. most cameras and human eyes), yeah, I think that’s a reasonable description. But it fails to account for the issues you can run into with global illumination: spectra that look identical to a given color observer can behave wildly differently when light bounces, differing illumination, etc. come into play. So it can actually make an enormous difference–even to the original color observer–in many circumstances.
In any case, I think we’re in agreement here. We’re just using different words to describe the same thing.
From my vantage, I am strictly speaking spectra here. Nothing “perceptual” beyond the fact that at some point we inevitably end up discussing these things relative to the CIE XYZ plot.
I’m very heavily of the belief that cameras can and do record spectra, and depending on the spectral filters, it can be “undone” back to the spectra, within some varying limitations.
There’s a line where the accuracy is “reliable” and “complete nonsense”, but by and large, I am a believer that spectral curves can do a sufficient job of inversion. Will it be a subset of the overall spectra? Of course. Will it be rather reliable in some regions and non spectral data in others where camera metamerism or IR / UV or voltage spill etc happens? Of course.
So I’m not at all discussing perceptual attribute here, and merely the ability to reconstruct the spectral radiometry from lookups, with caveats.
Within a reasonable degree of tolerance, I’d probably say I am on the disagreement side of this.
Hmm, okay. I think maybe we actually are in disagreement then. But I want to poke a little further to make sure. I swear I’m not being pedantic below, I’m just trying to establish some baseline assumptions.
Fundamentally, the whole idea behind metamerisms is that for any given color observer (e.g. a camera), there are different light spectra that will appear identical to it. Those light spectra can be wildly different from each other. A great example of how wildly different is, in fact, the RGB displays we use every day: they use three sharp-ish spikes of energy in the visible spectrum to cause us to see all kinds of colors that are normally (in the natural world) caused by very smooth spectra.
When trying to invert from RGB back to spectra, the task you’re facing is choosing one spectrum from the infinite and often wildly different spectra that could cause the original observer to see that RGB color. And this is a severely underconstrained problem.
It sounds to me, in your latest post, like you disagree with at least one of the things I’ve just written above. If not, then I’m misunderstanding you.
If you don’t disagree with anything I’ve written above, then actually, I think we’re still in agreement, and just talking past each other somehow.
I do want to clarify that, for reflectance spectra, I do believe that in practice we can often reconstruct close-enough spectra, by using additional assumptions (e.g. most natural reflectances are fairly smooth). And it will certainly result in much closer-to-real-life light transport than RGB rendering.
That’s exactly why the filter arrays are designed such that the overlaps are as unique as possible. It minimizes the many-to-ones as best as possible, leaving a combinatorial result.
Conventional camera A, B, C planes are solved to become virtual emissions. This is not what proper spectral tables deliver.
Again, it’s not perfect, but the results are much, much, much closer to spectral ground truth than RGB solves, which are a completely different kettle of fish.
This is a different discussion.
Again, this is about working backwards from say, a monochromator generated table. Given a decent spectral characterization of the sensor filters, you can indeed invert the process in a much more accurate way than the traditional RGB virtual emission approach. I’ll try to rustle up a plot if I can find some time.
I mean… as unique as possible is still not very unique, though. Given three (or even four!) types of filters in the array, maximizing the uniqueness of their overlaps still leaves you with the same problem I described earlier.
Perhaps my blunder in trying to communicate here was using the term “RGB”. What I’m actually talking about is precisely what you’ve outlined here: using a fully accurate spectral characterization of a color observer (e.g. a camera sensor) to aid in reconstructing spectra from the raw data output of that same observer. The problems I’ve been outlining are absolutely 100% relevant to that.
The issue is fundamentally about the nature of any capture device that transforms light spectra into a small number of values (e.g. the three values of most camera sensors). Even with a perfect characterization of the sensor, you simply don’t have enough data to accurately reconstruct an arbitrary visible-light spectrum.
To take this to first principles: what you’re talking about is taking potentially hundreds of values (the power spectrum of the light), baking it down to three values (the output of the sensor), and then un-baking those three values back into hundreds of values with reasonable accuracy. If someone has figured out a way to do that, then they have effectively invented an insanely efficient data compression scheme–far better than anything that exists today. There isn’t anything magical about light spectra or camera sensors that change this fundamental information theory problem.
Having said that, this problem only holds for arbitrary visible-light spectra. If you have further a priori information about your input spectra, you can use that to help achieve more accurate reconstructions. A good example of such information is that most natural reflectance spectra are fairly smooth. However, whenever your input spectra violate those additional assumptions, your reconstruction scheme will not be accurate.
They haven’t, but with that said, the spectral approach is an order of a magnitude more appropriate than the mathematical virtual primaries fit approach. And again, as with the caveats outlined, the approach “works”.
My vantage remains that spectral reconstruction from the ABC camera planes is by far more appropriate than the mathematical fitting approach.
I think we’d probably be in agreement there.
My bracelet testscene got corrupted somehow and the spectral Branch can’t open it anymore. (Blender silently crashes on file load) I can’t be 100% certain but I suspect there is some error with saving and the new nodes?
I can still open the file in Master but then the spectral nodes just become labelled as “Undefined” and if I try saving and then opening that, I just end up with that exact same Undefined nodes in the spectral branch too (as was to be expected)
If this is of any help, here is the file that is now broken:
https://www.dropbox.com/s/zmckz1n71mmflf8/Spectral%20Test%20Scene.blend
and here is the resaved version: Dropbox
I’ve noticed similar problem with spectrum curves node. The curve itself becomes corrupted when undoing changes and crashes blender when trying to change it, I guess you’ve got the same problem. I’ll look into it.
Hmm… so I’m back to thinking that we’re just talking past each other somehow, and it feels to me like we’re essentially going in circles at this point. I think either I’m misunderstanding you, you’re misunderstanding me, or (very likely) both. But I think we probably actually agree here, and are just approaching this from very different vantage points, which is making it difficult to communicate.
Some day we should grab a beer together with a sketch pad, and we can hash this out properly. But until then, I think I’m going to drop this for now. Especially since I think this is just clogging up the thread. ![]()
So I’m pretty sure I’m misinterpreting something but this is supposed to be Alexandrite with a yellow spectrum. The source I saw weirdly had yellow, green, pink, and blue Alexandrite all with essentially the same spectrum, with the biggest difference being the ratio of two peaks.
Alexandrite is famously a gem that looks very different under different lighting. I think you can see a little bit of that in action here in form of the significantly mroe yellowish green in the spots closest to the camera. But I think that something is clearly wrong here. Almost definitely due to me misinterpreting something.
Alexandrites look pink in one lighting and green in another. This render only features different (though arguably significantly so) shades of green.
I found a database of 1000+ spectra which I can actually read out as a table. It’s all reflectance spectra. This example is Rhodonite. It’s that kind of slightly orange pink which suddenly becomes a lot more saturated when specifically lit with orange light as you can see here (compare to the uniform light grey ground which only goes a mild shade of yellow)
I had a shot at Alexandrite after looking at your image and actually managed to get something pretty accurate (definitely looked red under some light and green under other) but then Blender crashed when undoing and the save was corrupt so there’s definitely some issue with the new nodes.
What’s the resource you found? It could be the sort of thing an addon could implement as a searchable database of spectra, so that it doesn’t have to be bundled with Blender.
It’s fascinating to see how light can interact in some cases like this. Great example.
I had to also download a free tool to access this. (It’s linked from that page) It asks you to register a name and mail and junk like that before downloading but it doesn’t actually check that stuff so you can fill it out with garbage.
However, it’s not free for commercial use as far as I could tell, so it’s not gonna be possible to package up all these example spectra in Blender I’m afraid. Still, it’s nice for testing purposes.
What I found, generally speaking, is that you’ll wanna look for “UV/Vis” spectra which cover the visible spectrum and the UV range.
Branch updates:
- updated Blender
- fixed crashes with “Spectrum Curves” node (old corrupted files will not open though)
- improved input range in “Spectrum Curves” node (x values are now in nm)
- removed output clipping from “Spectrum Curves” node
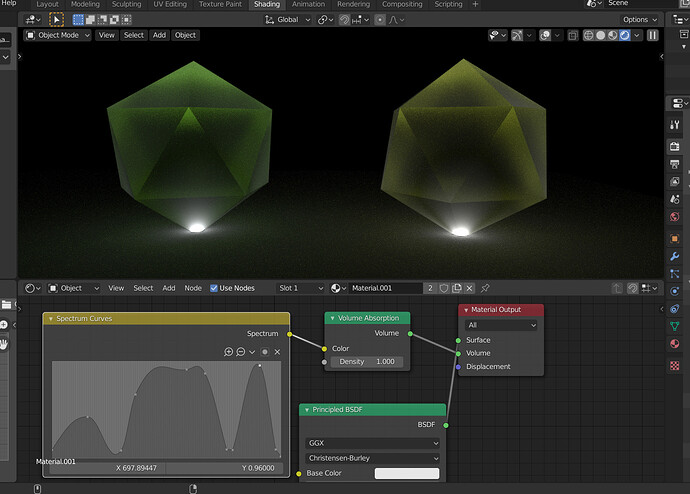
I think there’s an issue with absorption spectra in Blender right now.
Probably what’s going on is, that Blender takes 1 - the absorption spectrum as the actual absorption spectrum for the sake of artistic intuition? Like, if you want a pink absorbant material, you need to pick a pink color. And that makes a certain amount of sense for artists, but pyhsically, what that ought to mean, is that pink light is being absorbed and therefore absent from the material. It ought to render green.
However, absorption spectra don’t have to be limited to 1. They can grow arbitrarily large (though always positive). So I’m not quite sure what to do there: Will it be correct to simply go (Spectrum uniformly set to 1) - (Absorption spectrum)?
Because if the absorption spectrum shoots above 1, that would inherently yield negative absorption values which isn’t what’s supposed to happen, right? And if it’s exactly 1, that’ll yield a wavelength that will just be perfectly transmitted.
I’m not quite sure what to do about this. Thus far I simply put in spectra that don’t go beyond 1 and subtracted them from the uniform spectrum to get a reasonable color. But that’s not actually what’s supposed to be done, is it? I’m a bit at a loss as to what to do about this.
Does anybody with insight in the code have an idea how to deal with this correctly?