No I explained this before here:
You are approaching this purely from the lighting side, but there’s also a shading side to this, I’m saying that if a material is absorbing spectra, then in physical world that energy has to do something, it doesn’t magically disappear. One option is:
But I agree that it is a material property and has to be defined/built by the TD/lighting and shading artist. Having a ‘negative absorption value’ might give us a means of taking that value and doing something with it, as a feature.
Though the better question might be do we need to have it to achieve these things. If not then is it really a feature, or at least is it really a feature of value to us?
Bioluminescence specifically is a chemical reaction, hence a phenomenon of emission. It is created giving up energy obtained not from electromagnetic radiation, but from oxydation of an enzyme iirc. (unnecessary information, but bioluminescence fascinates me) So it really is its own light source and as such doesn’t warrant special treatment in the bsdf. …I think !
As far as I understand this differs from fluorescence (colour-wise) in that there is no spectral shift in the rendered energy.
I don’t think so?
As a general rule of thumb, every time something has been hard coded with a clamp / clip, badness ensues. It’s almost a universal constant, so I’d probably be against a default clipping / clamping even with the above belief. See RGB colour pickers in Blender, where a clamp was put into place and now there’s more problems with pixel management.
In terms of the practical side of negative spectra, there’s no upside to allowing them other than the pragmatic and sadly depressing reality that they can’t be avoided in some contexts. Clipping here actually will distort the data, so it’s wise to leave it “as is” and provide tools for overcoming the issues. This is no different than the exact same issues in the RGB encoding model.
Agree 100%. This is largely the domain of the BxDFs to handle. Fluorescence falls into this category. As would bioluminescence as an emission source perhaps. Under this lens, it’s identical to something like black body, where the numbers and model work out to some mechanism for energy output.
Spectral is a lot closer to RGB in many of these ways than people initially see. Within the path tracer, RGB is the radiometric-like energy quantity! It’s also why the entire RGB model is fundamentally and critically flawed of course, because RGB is implicitly based on a not-entirely-radiometric underlying model.
This is not what a negative spectrum conveys. It’s what a spectrum which puts values above 0 but strictly below 1 does. On bounces, spectra are multiplied. And in absorption they are too.
Technically, what’s happening is actually almost always kind of like flourescence: The atoms and molecular bonds and what not in any given colored material absorb some of the light and then re-emit it, commonly at longer wavelengths / lower energies. Namely most of the time in the infrared or lower - as heat. If you tallied up all this low energy light on top of what gets reflected away, you’ll end up with a perfect conservation of energy.
Visible-to-us flourescence is that idea but starting with high energy radiation usually beyond what we can see and thus giving enough of a gap to end with radiation in the visible spectrum. Absorbing UV radiation to re-emit it as visible light.
But in no such process does any spectrum ever go negative. Negative spectra just simply are not a thing in nature.
As said, I’m not against allowing it. I am, however, against making it all too easy. In 999 cases out of 1000 you would not want this.
There is another big common way to get colors, and that is refraction-based. Structural colors. Most blues in nature are actually of that sort. The sky is blue (as well as any of its other colors) because some sunlight is refracted by the atmosphere. Various animals and plants are almost always blue due to tiny features that give them very intense colors. Refraction spectra can often be incredibly saturated compared to absorption-based materials. They play by different rules. But even there: no negative spectra.
@LazyDodo In addition to the error you spotted, I also get this one right next to it:
/home/ubuntu/blender/intern/cycles/render/../util/util_types_spectral_color.h:31:67: error: ‘make_SPECTRAL_COLOR_DATA_TYPE’ was not declared in this scope; did you mean ‘SPECTRAL_COLOR_DATA_TYPE’?
31 | #define make_spectral_color(f) CAT(make_, SPECTRAL_COLOR_DATA_TYPE(f))
| ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~^~~
I think there has been one more, but the console output got trimmed.
I gave up the CentOS container, I was not able to bind my NVidia driver to it - something that works almost out of the box for Ubuntu.
(what a nice discussion on spectra, many thanks to all of you)
What the discussion mentions, but omits to explicitly define is the physically different nature of the various spectra. It is only after you give meaning to a spectrum that certain limits should be observed. For instance: a physical surface never reflects more light than it receives so reflectance must be between zero and one. Attenuation by absorption is physically defined as a fraction of photon absorption events along a length of medium and must therefore always lie between zero and one (and via Lambert-Beer features absorption coefficients between zero and positive infinity). Physical Phosphorescence- and fluorescence events alter a photon wavelength (and therefore its energy) in a probabilistic manner and will always obey conservation of energy (at the wavelength/eV level) between the input and output spectral distributions.
But otherwise, much like any number in mathematics, spectra too can be manipulated any way you like. In that sense, artists are free to abuse those spectra any way they like. But sure: they should be warned by the UI when they go beyond the physically plausible range of values.
Cycles, the physics-based renderer, should obey the rules of physics by observing the definitions of the various spectra. For instance: the BxDF nodes should assume that their input sockets provide values that are within those physics definitions and the BxDF should compute by those definitions to produce its outputs. But very important to artists: the same BxDF should (with sufficient warning) allow inputs outside the physically plausible range and should behave in some predictable (albeit nonsensical) manner.
Maybe, checking a box at the node-UI would force clamping of the inputs. An unchecked box would be highlighted to state a warning.
Of course spectra in general can be what ever they need to be. This is specifically the spectrum of light we’re talking about. And throwing unphysical values into physical equations can be summarized by. “garbage in garbage out”.
In this case what you get is actually still kinda predictable, but what it is is effectively the non-conservation of energy. Absorption which adds light that shouldn’t be there. Light sources which emit photons that remove light instead of adding it. Those kinds of effects.
They could be interesting to explore in very limited settings. But almost never are they gonna be what an artist actually wants.
That being said, I think the UI solution is easy enough for the most part:
Make stuff like that have a default range you can easily drag around your values in, which is physically reasonable.
But, as is the case in many places in Blender, you could simply type in an out-of-range value and Blender will do that as well.
Maybe additionally having some sort of non-physicality warning would be a good idea, but otherwise nothing special is needed
Indeed. I think the exploration of the very limited settings should be motivated by either the limits of mathematics or the limits of artistic predictability.
I do not quite agree with the idea that reflection is a pure surface effect only.
Yes, when study the physics behind pure reflection there are three sub-types: reflection at a dielectric interface (glass/air, air/water, …), reflection at a conductor interface (aluminium/iron, …), and reflection at a dielectric/conductor interface (air/iron, water/copper, …). Whenever a conductor is in play, the quantum (or wave) mechanics about the interface take a few wavelengths to stabilize and beyond those few wavelengths, it looks like it is instantaneous. At a pure dielectric interface, the quantum (or wave) mechanics play within half a wavelength. All three of these cause what many would call the ‘glossy reflection’. It is the differentiating factor between buying high-gloss and matte paint of the same color. It is what the Principled BSDF calls the ‘clearcoat’ and ‘metallic’. The same Principled BSDF provides a ‘Base Color’, which is non-physical for the following reason:
No, when light does pass through a dielectric interface, it will encounter the particles that make up the bulk of the object (i.e.: the medium); the pigment so to say. If those pigment particles do not absorb light but only scatter it about, then some light will be scattered back outward of the object through the dielectric interface where it came from. This makes white paint indeed white instead of transparent. When the pigment also absorbs light (most often more at one wavelength than another) the sum light energy is reduced before the light is scattered back out of the object. This makes (say) blue paint instead of white. So this type of reflection is actually a subsurface volume effect too. In daily conversation however, the amount of pigment determines whether one claims to observe surface reflection or sub-surface reflection and the presence of a dielectric interface would add a remark on glossiness.
To complete the outline above, I should include pure Lambertian bulk in which there are no pigment/particles but the medium does absorb some fraction of the incident light. In that case, there is no scattering and all reflection will be of the pure form.
It’s not so much an issue of intentionally limiting what is possible in the engine, the issue lies in defining predictable and practical behaviour of negative values within a spectrum in different scenarios. For example, what does it mean for a diffuse material to absorb more than 100% of the incident light? Once you’ve absorbed 100% of the light, what else is there to absorb? If someone can come up with a logical, practical and useful answer to that question, then I’m sure implementing it in the engine would not be so difficult.
It’s less about physically plausible (which is a goal of every realistic render-engine) and more about making the behaviour defined. Undefined behaviour is what I’m facing here, as opposed to out-of-gamut RGB triplets which are well-defined and predictable within their scope of use.
Sure, if you look closely enough, what I’m saying ends up no longer quite holding true. But for the purposes of how Cycles handles light, incoming light (whether it’s based on three primaries or entire spectra) is, for the most part, simply multiplied by the surface color (its three assigned values, or its entire spectrum) a single, instantaneous time. Cycles handles neither relativistic nor quantum effects (unless they are specficially encoded in a BSDF which could, in a very limited capacity, happen) - there are some exceptions such as Multiscatter GGX which, true to its name, actually simulates multiple bounces on a surface based on its roughness values.
And sure, scattering effects also happen gradually. Those work by assigning a different scattering probability to each wavelength. Some wavelengths will scatter faster and therefore diffuse out rather than stay focused, effectively getting darker in one spot and brighter in another. At high enough scattering, light has a reasonable chance of getting captured in a material effectively forever (at least for long enough to exceed the bounce limit), thereby making that light invisible to the camera. (Or, technically, the camera-emitted ray won’t ever find a light source to connect to) and causing a return type of blackness.
By the way, I’m not sure what a negative spectrum would mean for scattering. I think the way that works is effectively a form of clamping? Like, if scattering density is a form of probability somehow (I’m not sure, it might be the mean scatter event frequency or the inverse mean path length?), if that goes negative, it might simply be like a frequency identical to 0, i.e. no scattering at all, or else it might be like the same frequency but positive, in which case sign literally wouldn’t matter there. I’m really not sure and which one happens would probably be implementation-specific, depending on the algorithm chosen for simulating this.
What happens there is the same as with negative light sources, I think: You’ll end up reflecting away negatively-valued photons which effectively eat up light. Like, this would be a material that’s so dark, that its bouncelight would further darken other stuff!
Except there is a problem: What happens if your bounce light is already negative? Suddenly, those photons will go positive. So really, negatively reflective materials are going to continuously switch between positive and negative light rays. And that’s gonna mess with certain assumptions Cycles puts on light:
By, now, default, Cycles will probabilistically cancel light paths that are dark enough to be unlikely to contribute to the image. So such light paths are likely to just be stopped, I think. Cycles won’t converge to the correct result concerning these anyways. In so far as there even is a correct result in the first place.
Maybe if probabilistic light path termination is deactivated (Set light sampling threshold to 0), it might end up doing “the right thing” in this wrong situation? I’m not sure. I’d not be surprised if positive light is assumed in other spots as well.
Really, fluctuating values like that usually mean no convergence at all. Literally any value could happen in such situations. Or at the very least a set of values that all are “correct” endpoints (stuff would converge into a loop of sorts, fluctuating between two or more different values) and you’d somehow have to show all of them when an image can only ever have a single value per pixel. It’s simply illdefined.
Negative light sources I can almost accept. They could behave stably in the same way that they’re used in RGB cycles, that is, they start out as some negative number, and they get attenuated just like regular light, but then when they are accumulated on the film, their contribution is L*A where L is the negative light brightness and A is the attenuation ratio. This way it does indeed behave stably and have predictable results, doing what you say and ‘sapping’ the light from the film where it lands.
Negative RGB diffuse also makes sense to me in the same context, you take a light brightness, multiply it by a negative number and send it on it’s way, from that point forward it acts like negative emission. If it then bounces into another negative coloured material, it’ll become positive again, but since this is very unlikely, the render would still resolve.
Maybe we could treat negative spectra in the same way, I can see it working now, actually, but it just doesn’t relate to anything in the physical world. Again, comparing that to negative colours in RGB cycles, they’re just any colour that’s out of gamut. Negative spectra are something much more far-fetched, but they could behave in the same way, I suppose.
I don’t think you have to do anything special there: Negative spectra WILL behave that way already. The only difference is that your originally three lights turned into a continuum of lights corresponding to each wavelength in the visible range.
But as said, negative diffuse, because of its chance to fluctuate light sources back and forth, are really not stable. Pathtracing simulates physics by convergence, but in the presence of negative reflection, convergence to a single point is no longer guaranteed. Instead, you get convergence to some sort of attractor set or even outright divergence.
I wouldn’t say it’s particularly unlikely to have repeat negative bounces if there is even a single negative-reflectance material somewhere. How unlikely that is fully depends on your scene, and even in your average scene involving diffuse materials, repeat backbounces aren’t unheard of. Three-bounce contributions would be enough to cause this.
Luckily, usually, most contribution happens in the first bounce, and almost all happens in the first two bounces. But this isn’t an assumption we can actually make in general. Especially in the presence of reflectance spectra greater than 1 (or less than -1), in which case, additionally to it fluctuating back and forth, the effect will become stronger and stronger over time.
And I still have no idea how exactly scattering volumes would be handled in these cases.
Negative values don’t work in RGB nor in spectral. At all. They break things.
With that said, they are equally unavoidable in some contexts, so must be accounted for and negotiated.
I tried to do something equivalent to the absorption tests from before but this time with scattering.
So Rayleigh scattering, which is the type of scattering which gives the sky its blue color, has a scattering spectrum that just happens to be similar to blackbody radiation in the limit of infinitely high temperature.
I can’t quite get that, but I sure can try putting in ridiculously high temperatures as a proxy.
Effectively, that gives me the ability to roughly simulate how sunlight is scattered by the sky:
The light source on the left is a sun lamp with angle 0° (so light is initially entirely parallel) and blackbody temperature of 5777K (equivalent to our sun), the scattering spectrum of the medium is from a 22000K blackbody which is, of course, nowhere near infinity, but it should be close enough.
From bottom to top, density increases exponentially from 0-99, so at the bottom you see how this would look like in space, with no atmospheric scattering, and as you travel up, scattering becomes more and more intense, effectively giving rise to the colors of the sky at noon or twilight.
The block is 1BU thick and the height and width here cover 10BU
It looks like scattering spectra similar to cold blackbodys (meaning warm colors) actually end up being roughly similar to geometric scattering (where particle sizes are much bigger than the scattered wavelenghts - think rainbows), very hot ones (bluish) like this are similar to Rayleigh scattering (particles are much smaller than the associated wavelenghts as in the sky), and in between, the roughly neutral looking spectra give results akin to Mie scattering (particles are roughly the same size as the scattered wavelengths, think clouds)
I don’t think that actually is reasonable for Geometric and Mie. It just so happens to give similar results. But for Rayleigh it actually roughly checks out!
Here is an example somewhat like Mie scattering:
(5777K for the scattering spectrum. It’s basically like fog. Very slightly greenish on the bottom)
Finally, herer’s a more rainbow-like version as geometric scattering might cause:
This is with a spectrum corresponding to blackbody temperature 2000
You can get a cleaner rainbow (i.e. with very visible red and purple) if you go for lower temperatures. However, to get into the purple range requires scattering densities well above 100 and apparently that’s roughly where the same kind of issues begin that I already found for absorption. Much earlier than there. Absorption was quite stable up to densities of 10^6.
(The problem is that values suddenly start exploding, growing way out of gamut but also way too bright. I’m surprised that scattering will have that happen this early. 100 doesn’t seem like a number big enough to cause serious floating point issues)
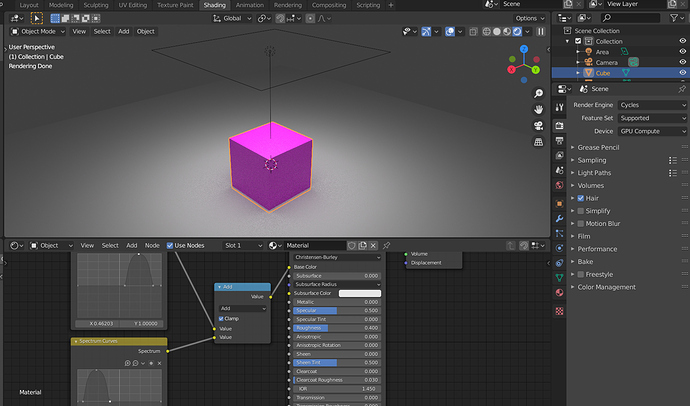
CUDA kernels and Linux builds should compile now. Also, new “Spectrum Math” node can be found in “Spectral” nodes category.
I’m still getting the following error (on Focal Fossa):
/home/ubuntu/blender/intern/cycles/kernel/osl/../../util/util_types_spectral_color.h:31:36: error: ‘make_SPECTRAL_COLOR_DATA_TYPE’ was not declared in this scope; did you mean ‘SPECTRAL_COLOR_DATA_TYPE’?
31 | #define make_spectral_color(f) CAT(make_, SPECTRAL_COLOR_DATA_TYPE(f))
| ^~~~~
I temporarily fixed it by removing the CAT and using
#define make_spectral_color(f) make_float8(f)
//same fix for the rest
Btw it’s definitely not a good idea to call a function CAT since full text search in the repository returns everything else related to cats but not its definition.
So the next error I’m getting is this one:
/home/ubuntu/blender/intern/cycles/kernel/../util/util_math_float8.h:433:17: error: ‘_mm256_pow_ps’ was not declared in this scope; did you mean ‘_mm256_xor_ps’?
433 | return float8(_mm256_pow_ps(v.m256, _mm256_set1_ps(e)));